Integral infinity
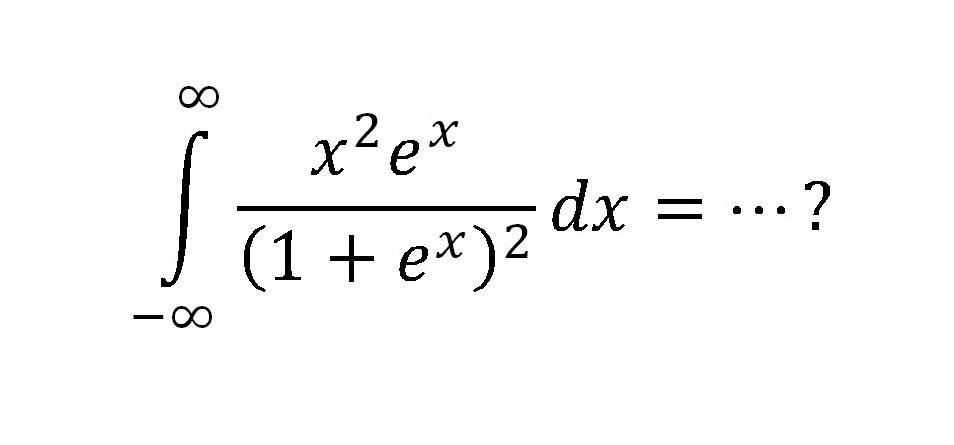
Main post link -> http://www.facebook.com/photo.php?fbid=3272444470312&l=c9af88f8c1
No vote yet
1 vote
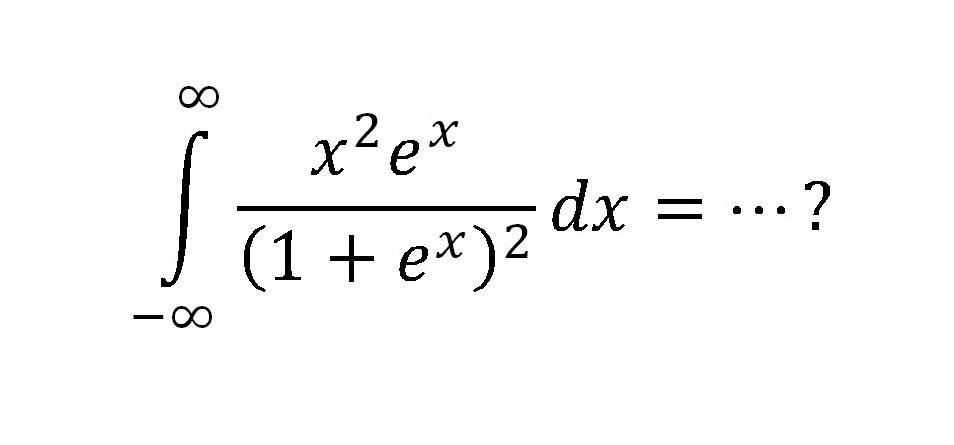
Main post link -> http://www.facebook.com/photo.php?fbid=3272444470312&l=c9af88f8c1
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
Let S denote the value
Since the integrand is an even function
S = 2 * integrate(0 to infinity) x^2 e^x /(1 + e^x)^2 dx
Apply integration by part, let u = x^2 => du = 2x dx, dv = e^x /(1 + e^x)^2 => v = -1/(1 + e^x)
S/2 = uv - integrate v du
S/2 = -x^2 /(1 + e^x) + 2 integrate(0 to infinity) x/(1 + e^x) dx
Apply the limits from 0 to infinity for -x^2/(1 + e^x), you get 0
S/4 = integrate(0 to infinity) x/(1 + e^x) dx, divide top and bottom by e^x
S/4 = integrate(0 to infinity) xe^(-x) /(1 - (-e^(-x)) dx, this is in the form of a/(1-r), sum of a geometric series
S/4 = integrate(0 to infinity) [ xe^(-x) - xe^(-2x) + xe^(-3x) - xe^(-4x) + ... ] dx
Notice each term follows a Gamma Distribution with alpha = 2, beta = 1/1, 1/2, 1/3, ....
It simplfies to
S/4 = (1/1)^2 - (1/2)^2 + (1/3)^2 - (1/4)^2 + ...
Right hand side is a form of Riemann Zeta function of 2
S/4 = pi^2 /12
S = pi^2 /3
Note that (1/1)^2 - (1/2)^2 + (1/3)^2 - (1/4)^2 + ...
= [ (1/1)^2 + (1/2)^2 + (1/3)^2 + (1/4)^2 + ... ] - 2 [ (1/2)^2 + (1/4)^2 + (1/6)^2 + ... ]
= [ (1/1)^2 + (1/2)^2 + (1/3)^2 + (1/4)^2 + ... ] - (1/2) [ (1/1)^2 + (1/2)^2 + (1/3)^2 + ... ]
= (1/2) * [ (1/1)^2 + (1/2)^2 + (1/3)^2 + (1/4)^2 + ... ]
= (1/2) * pi^2 /6 = pi^2 /12
Log in to reply
may you explain why it can be this.
Notice each term follows a Gamma Distribution with alpha = 2, beta = 1/1, 1/2, 1/3, ....
thx before :D
Log in to reply
integrate(0 to infinity) [ xe^(-x) - xe^(-2x) + xe^(-3x) - xe^(-4x) + ... ] dx
= integrate(0 to infinity) [ xe^(-x) ] dx + integrate(0 to infinity) [ xe^(-2x) ] dx + integrate(0 to infinity) [ xe^(-3x) ] dx + integrate(0 to infinity) [ xe^(-4x) ] dx + integrate(0 to infinity) [ xe^(-4x) ] dx + ...
All the integrand are in the form of a gamma function of x^(alpha - 1) * e^(-x/beta)
So alpha = 2 for all integrals, beta = 1/1, 1/2, 1/3, 1/4, ....
Log in to reply
ok :D i very understand it thx you so much :D