Interesting Problem
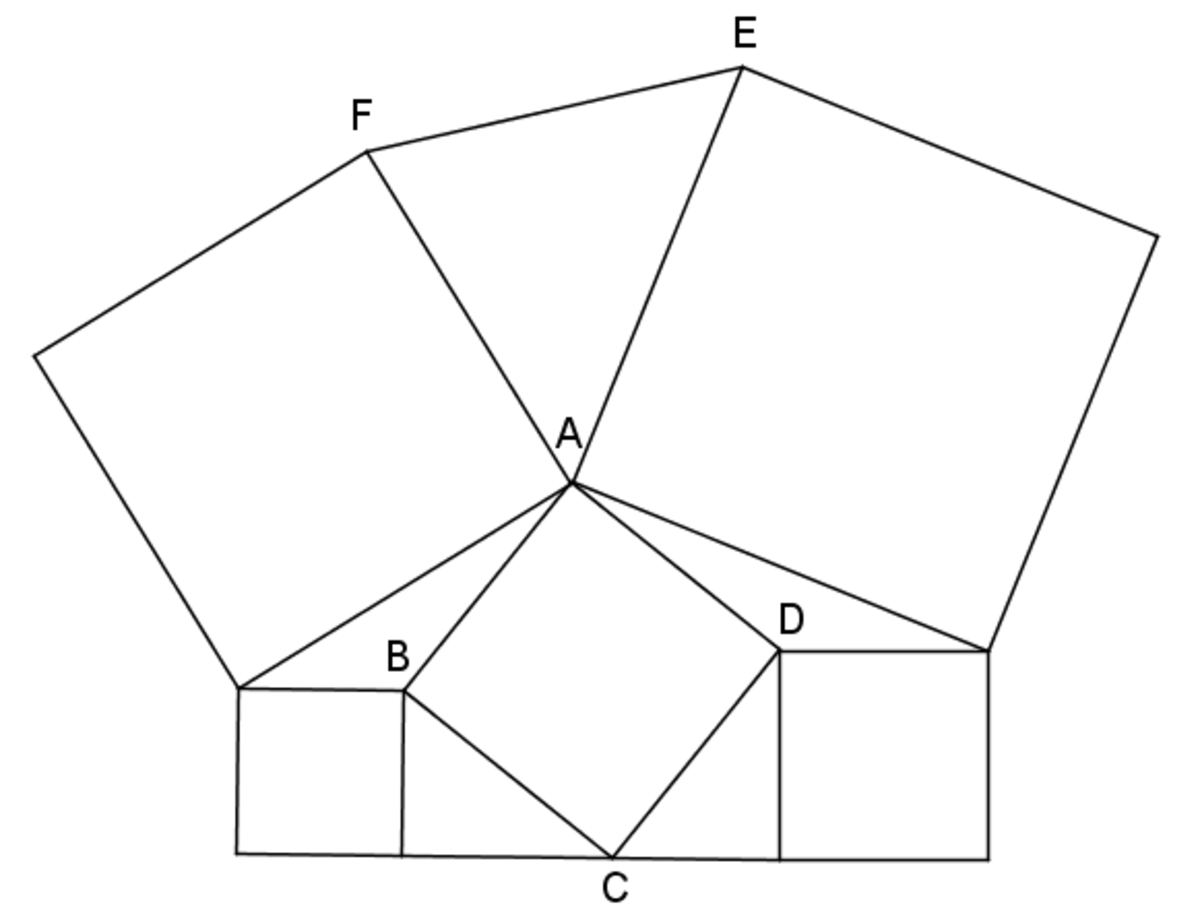
Hey Brilliant, I found this interesting problem in Catalonia's Olympiad.
We have five squares stowed in this way: (See the photo)
Prove that ABCD sqare has the same area as AEF triangle.
No vote yet
2 votes
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
If ABCD has side x, then BX=xcosθ and DY=xsinθ. Since ∠ABX=180∘−θ and ∠ADY=90∘+θ, we deduce from the Cosine Rule that y2z2==x2+x2cos2θ−2x2cosθcos(180∘−θ)=x2(1+3cos2θ)x2+x2sin2θ−2x2sinθcos(90∘+θ)=x2(1+3sin2θ) Using the Sine Rule on ABX and ADY, sinαsinβ==yxcosθ×sin(180∘−θ)=1+3cos2θsinθcosθzxsinθ×sin(90∘+θ)=1+3sin2θsinθcosθ and hence cosα=1+3cos2θ1+cos2θcosβ=1+3sin2θ1+sin2θ Hence cos(α+β)=(1+3cos2θ)(1+3sin2θ)(1+cos2θ)(1+sin2θ)−sin2θcos2θ=(1+3cos2θ)(1+3sin2θ)2 Now γ=90∘−α−β and so sinγ=cos(α+β). Thus ∣AEF∣=21yzsinγ=(1+3cos2θ)(1+3sin2θ)yz=x2=∣ABCD∣
There's no need to bust out the complicated trigonometry. ;)
We note that X′A=XA, AB=BC=CD=DA and Y′A=YA. Also ∣BCV∣=∣XBA∣=∣ADY∣, which can be easily proved by trigonometry--noting that ∣BCV∣=21×BV×BC=21×BX×BA=∣XBA∣ and the same can be done for triangle ADY.
We construct X′B′A by rotating XBA 90 degrees clockwise about A and X1′B′C by rotating XBA 90 degrees clockwise about B. Similarly we construct Y′D′A by rotating YDA 90 degrees anticlockwise about A and Y1′B′C by rotating YDC 90 degrees anticlockwise about D.
Rotation preserves area and congruency, and we see that by angle chasing, X′B′ is equal in length and parallel to X1′B and the same with the pairs B′D′ and BD, Y′D′ and Y1′D. Therefore we see that X′Y′D′AB′ is congruent to X1′Y1′DCB.
More importantly we also see that ∣BDHV∣=∣X′Y′D′B′∣=∣X1′Y1′DB∣ as all three share the same height VH and lengths BV and DH.
Therefore
∣X′Y′A∣=∣X′Y′D′AB′∣−∣X′B′A∣−∣Y′D′A∣=∣X1′Y1′DCB∣−∣X1′BC∣−∣CDY1′∣
=∣X1′Y1′DB∣+∣BCD∣−∣BVC∣−∣DCH∣=∣BDHV∣+∣BCD∣−∣BVC∣−∣DCH∣
=∣BCD∣+∣BVC∣+∣DCH∣+∣BCD∣−∣BVC∣−∣DCH∣=2∣BCD∣=∣ABCD∣
And we are done! ;)
Log in to reply
I forgot to add in sin∠BVC=sin∠XBA as ∠BVC=180−∠XBA. Oops. ;)
This is obvious, but the area of ABCD equals the sum of the areas of the two smallest squares. I don't know if that would help though.
EDIT: I played with the problem a little bit. Label the side of the smallest square to the side of the biggest square a-e, respectively. After tinkering with the Pythagorean Theorem, I have come to the conclusion that 5c2=d2+e2, so if you can prove that 5d2+e2 is the area of ΔAEF then you are done.
Do the two lower squares have coincident bottom sides, and does C lie on the extension of both bottom lines?
Log in to reply
I think we can assume that. If it wasn't the case, the figure would probably have been drawn differently.
wow so complex
teach me your ways master