Introduction to Cryptography Part-2 (Diffie-Hellman Key Exchange system)

This the second installment in my series of post related to modern cryptography...Click here for part 1 on RSA ciphers

Introduction

$\textbf{Introduction:-}$Most ciphers require the sender and the receiver to exchange a key prior to exchanging coded messages.But the key which is exchanged may itself be vulnerable to attack by an unauthorized third party while it is being transmitted over a network.So serious effort is essential to ensure the safety the safety of the key so that it does not all into the wrong hands.

key

$\textbf{An Analogy:-}$Suppose two people Alice and Bob want to exchange a secret.So at first Alice puts the secret in a box and locks it up using a padlock(which only she can unlock) and sends the locked box to Bob.Bob who is unable to open the padlock puts another padlock on the box(which only he can open and sends the box back to Alice.Now Alice receives the box with two padlocks and she opens up her padlock and returns the box to Bob.Notice that now the box only contains Bob's padlock.After receiving the box Bob opens up his own padlock and hence opens the box containing the secret.

Imd

$\textbf{ALGORITHM(Diffie-Hellman):-}$

Step 1. Together Alice and Bob choose a 200-digit number p which is likely to be a prime and a number $g$ such that $1 < g <p$

$\textit{Step 2.}$Alice secretly chooses an integer $n$

$\textit{Step 3.}$Bob secretly chooses an integer $m$

$\textit{Step 4.}$Alice computes $g^{n} \mod p$ and tells that to Bob.

$\textit{Step 5.}$Bob computes $g^{m} \mod p$ and tells that to Alice.

$\textit{Step 6.}$The shared secret key is now $s \equiv (g^{n})^{m} \equiv (g^{m})^{n} \equiv g^{mn} \pmod{p}$

Notice that both Alice and Bob can easily compute it. Alice computes this as $s \equiv (g^{m})^{n} \equiv g^{mn} \pmod{p}$ Bob computes this as $s \equiv (g^{n})^{m} \equiv g^{mn} \pmod{p}$

Now they can communicate with each other using their agreed upon secret key by encrypting messages using a suitable cipher(like Arcfour,Bowfish,Cast128 etc).

$\textbf{Safety and the Discreet Log problem:-}$ in order to understand the conversation between Alice and Bob the eavesdropper needs the shared secret k $s$.BUt it is extremely difficult to compute $s$ given only $p,g,g^{n} \mod p,g^{m} \mod p$.One way to compute would be to compute n from the knowledge of $g$ and $g^{n}$ bt for extremely large values of p this is computationally in-feasible.A polynomial time bound in a quantum computer was provided by Peter Shor.This is known as the $\textit{Discreet Logarithm problem}$.

Part of the reason why this is difficult is because the logarithm of real numbers is continuous but (minimum) logarithm of a number $\mod p$ bounces around at random.

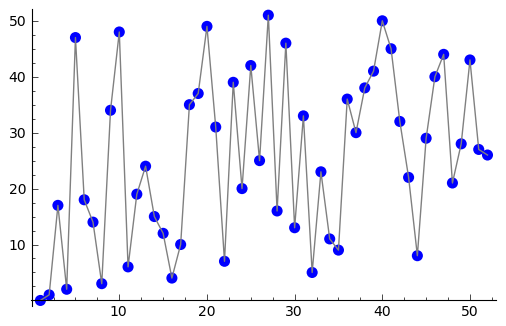Img

The above plot shows this exotic behavior.

$\textbf{Man in the middle attack:-}$ Suppose when Alice is sending a message to Bob announcing $g^{n} \pmod{p}$, a mamn(eavesdropper) intercepts the message and sends his own number $g^{t} \pmod{p}$ to Bob.Eventually Bob and the man agree on a secret key $g^{tm} \pmod{p}$ and Alice and the Man agree upon the key $g^{tn} \pmod{p}$.

When Alice sens a message to Bob she unknowingly uses the secret key $g^{tn} \mod p$,the man intercepts it decrypts it,changes it and re-encrypts it using the key $g^{tm} \mod n$ and sends it to Bob.This is bad because the man can now read every message between Alice and Bob and moreover can change them in submission in subtle ways.

hacker

One way to get around this attack is to use the Digital Signature Scheme based on the RSA Cryptosystem.

Please reshare as much as possible if you want more such posts on modern cryptography!!Feel free to ask any questions related to this in the comments ...and if you want to make another series of notes alongside this cryptography series then post your suggestions in the comment box.

Have a nice day!! :)