Introduction to partitioning of integers(Part 1)

As this is my first note for the Torque Group any feed back from the staff and also my fellow users is welcome.

$\textbf{Q.}$Let $n$ be a positive integer.In how many ways can one write a sum of (at least two) positive integers that add up to n?Consider the same set of integers written in different order to be different.

$\textbf{Ans.}$ Consider the $n-1$ spaces between $n$ 1's in the following arrangement : 1_1_1_1........_1

In each of the spaces either we put "+" or we put ")+(".The number of ways to do it is $2^{n-1}$.It is to be noted that each of these arrangements correspond to a unique way of partitioning n.This happens because by order of operations we need to add the numbers between each pair of parentheses first.

For example, for $n=8$, $(1+1)+(1+1)+(1)+(1+1+1) = 2+2+1+3 = 8$

Among the different possible combination the only one that does not correspond to a legal sum is = $(1+1+1+1+1+...+1)=n$.

So the total number of possible ways is $2^{n-1}-1$

A much more interesting idea is the number of ways in which one can write a sum of integers that add up to n, if different orders of summands are not distinguished.In this series of post I will try to provide a overview of this topic while introducing a few techniques for dealing with them.This will hopefully shed some light on the beauty of the subject for you.

$\textbf{Definition:-}$A partition of an integer n , is one way of writing n as a sum of positive integers where order of the addends(terms to be added) does not matter.For the integer $n$ the function giving the number of partitions is denoted by $p(n)$.

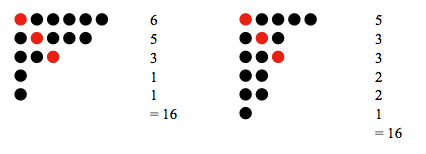
As shown below there are 7 partitions of 5.Thus $p(5) = 7$.

$5 = 5$ $5 = 4+1$ $5 = 3+2$ $5 = 3+1+1$ $5 = 2+2+1$ $5 = 2+1+1+1$ $5 = 1+1+1+1+1$

$\textbf{Ferrer's Diagram(A pictorial representation):-}$A Ferrer's diagram is a way of visualizing partitions with dots.Each row represents one addend in a partition.For example ,The partition of $16$ into $6+5+3+1+1$ and into $5+3+3+2+2+1$ is shown in the given diagram.

Here are a few problems that can be solved using Ferrer's diagrams please post your solutions in the comments.

$\textbf{Problem 1}$. Show that the number of partitions of an integer $n$ into parts the largest of which is $r$ is equal to the number of partitions of $n$ into exactly r parts.

$\textbf{Problem 2}$. Prove that every number of the form $n^{k}$ where $n$ is an integer greater than one and $k$ is a positive integer can be represented as the sum of $n$ positive odd integers.

$\textbf{Problem 3}$. Prove that the number of partitions of $n$ with no part greater than $k$ is equal to the number of partitions of $n + k$ with exactly $k$ parts

In the next post I will introduce generating functions in association to solving partition problems and in another post I will discuss stacking problems.Good Day!!

Click here for part 2