Inverse Trigonometric Functions

Definition

Inverse Trigonometric Functions are, like any other inverse function, mathematical operators that undo another function's operation.

Given a triangle like this

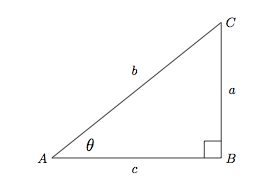Triangle ABC

the basic trigonometric functions would be defined as:

$\begin{array}{lcr} \sin \theta = \frac{a}{b} & \cos \theta = \frac{c}{b} & \tan \theta = \frac{a}{c} \end{array}$

with the angle as their input (or argument) and a ratio of sides as their result. However, the inverse functions take the ratio as input and return the angle:

$\sin^{-1} \left( \frac{a}{b} \right) = \theta \\ \cos^{-1} \left( \frac{c}{b} \right) = \theta \\ \tan^{-1} \left( \frac{a}{c} \right) = \theta$

This means the inverse trigonometric functions are useful whenever we know the sides of a triangle and want to find its angles.

Note: The notation $\sin^{-1}$ might be confusing, as we normally use a negative exponent to indicate the reciprocal. However, in this case, $\sin^{-1} \alpha \neq \frac{1}{\sin \alpha}$. When we want the reciprocal of $\sin$ we use $\csc$. In order to avoid this ambiguity, sometimes people might choose to write the inverse functions with an arc prefix. For example:

$\arccos \beta = \cos^{-1} \beta$

Technique

In following statement, $a$ and $b$ are positive, co-prime integers. What is the sum of $a$ and $b$?

$\cos^{-1} \frac{17}{\sqrt{1130}}= \tan^{-1} \frac{a}{b}$

Since we are trying to find $a$ and $b$, we should take the tangent of both sides of the equation:

$\begin{aligned} \tan \left( \cos^{-1} \frac{17}{\sqrt{1130}} \right) &= \tan \left( \tan^{-1} \frac{a}{b} \right) \\ \tan \left( \underbrace{\cos^{-1} \frac{17}{\sqrt{1130}}}_{\large{\theta}} \right) &= \frac{a}{b} \end{aligned}$

Further, we we can use the ratio given to sketch the triangle with $\theta$ in it, using the definition of $\cos^{-1}$:

Right Triangle with side 17 and hypotenuse square root 1130

Now, using the Pythagorean theorem, we can see that $17^2 + a^2 = 1130$. This means $a=\sqrt{1130-289}=29$. Finally, we evaluate $\tan \theta = \frac{29}{17}$, which means $a+b=46$. $_\square$