Is there a pure geometric solution to this problem?
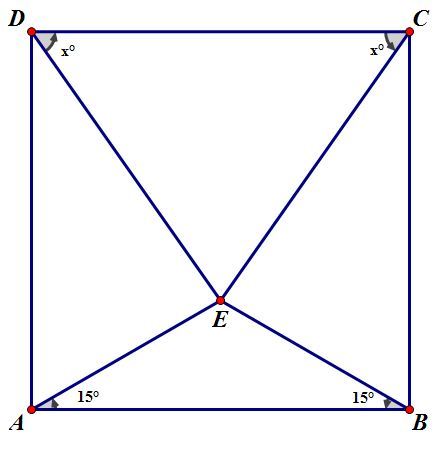
ABCD is a square. And there is a point E such that angle EAB = 15 and angle EBA = 15 degrees. Show that EDC is an equilateral triangle. Now there is a proof by contradiction solution to this problem. I was wondering if there is a pure geometric solution too(no trigonometry)?
No vote yet
1 vote
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
Proof by contradiction I meant: let angle EDC =x, angle DEC=(180-2x), angle EDA=(90-x), angle DEA=(x+15). Now suppose that x >60. Then 3x>180 therefore x>(180-2x). Therefore angle DCE>angle DEC. Therefore DE>DC. Also, x+15>75, so in triangle DEA we have angle DEA>angle DAE. Therefore AD>DE. Thus we have AD>DE>DC, an absurdity because AD=DC! Likewise for x<60. So the only option left is to conclude x=60 and this means triangle DEC is equilateral.
Construction of a similar 15deg triangle on BC. Ie. BFC. Then BFE is equilateral. Then by congruency you can do it. Instead of proving CD=CE, prove that CB=CE. Sorry I'm slow with formatting so can't post entire solution. Hope you understand it.
I too searched a purely geometrical solution of it. I ended up using atleast the ratio of sides of a right triangle, which i guess not geometry... But let's see if someone comes out with a nice solution.... :)
I see it as a pyramid (3D), just looking at the angles we cant really say it as equilateral. But an isosceles!
You can also do it by area. Though I don't know whether that qualifies for "geometry".
Here is a geometric solution provided by Dr.Shailesh Shirali to me(along the lines suggested by Lavisha Parab):
Draw a copy of triangle EAB with DA as base. That is, locate point F inside the square such that triangle FDA is congruent to triangle EAB.
Then angle FAD = angle EAB = 15 deg, so angle FAE = 60 deg. Also, FA = EA. Hence triangle FAE is equilateral, and angle AFE = 60 deg, and FA = FD = FE.
Therefore F is equidistant from A, D, E and so is the circumcentre of triangle DAE.
Therefore by the circle theorems, angle AFE = 2 angle ADE.
But angle AFE = 60 deg. Hence angle ADE = 30 deg, and it follows that angle CDE = 60 deg. So triangle CDE is equilateral.
(I am unable to upload or paste the jpg of the above solution)
x=arctan[2-tan15]