Is Trignonometry part of Geometry?

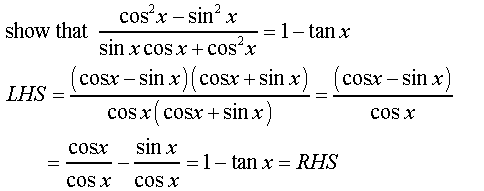
I don't use to consider a problem whose solution involves only trigonometric manipulations as "geometrical". For me such problems reflect more the algebraic skills not the geometric thinking.

This is relevant if we focus on training the "thinking"...

What dou you think?

#Geometry #Trigonometry

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

isn't this similar to asking if analytic geometry is geometry? I guess it depends on the focus. If algebraic manipulations are the core of the problem, then not (it's just the clothing). I have even seen trigonometry problems solved by pigeon hole principle (so it's really a combinatorics problem dressed as trigonometry). But sometimes, specially when you work with sines' law and the alike, geometry is more evident.

omm yucatan - 6 years, 11 months ago

Trigonometry has always been geometry, though it has been hijacked over the last 300-400 years by calculus and analysis. The modern idea of "sines" and "cosines" are relatively new, and the foundations of trigonometry are not built upon them. For want of a better summary, to define an "angle" properly requires a valid notion of orientation and "arclength", and hence limits yourself to rays instead of lines (there will be eight different definitions of angles between two lines). Moreover, infinite power series are required to precisely define "sine" and "cosine", as a result of independent works by Taylor & Maclaurin.

I contend and firmly believe that we ought to abandon the current framework for trigonometry and consider a purely linear algebraic approach to the subject, hereby involving vectors.

A Former Brilliant Member - 2 years, 10 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$