Isosceles Triangle Problem

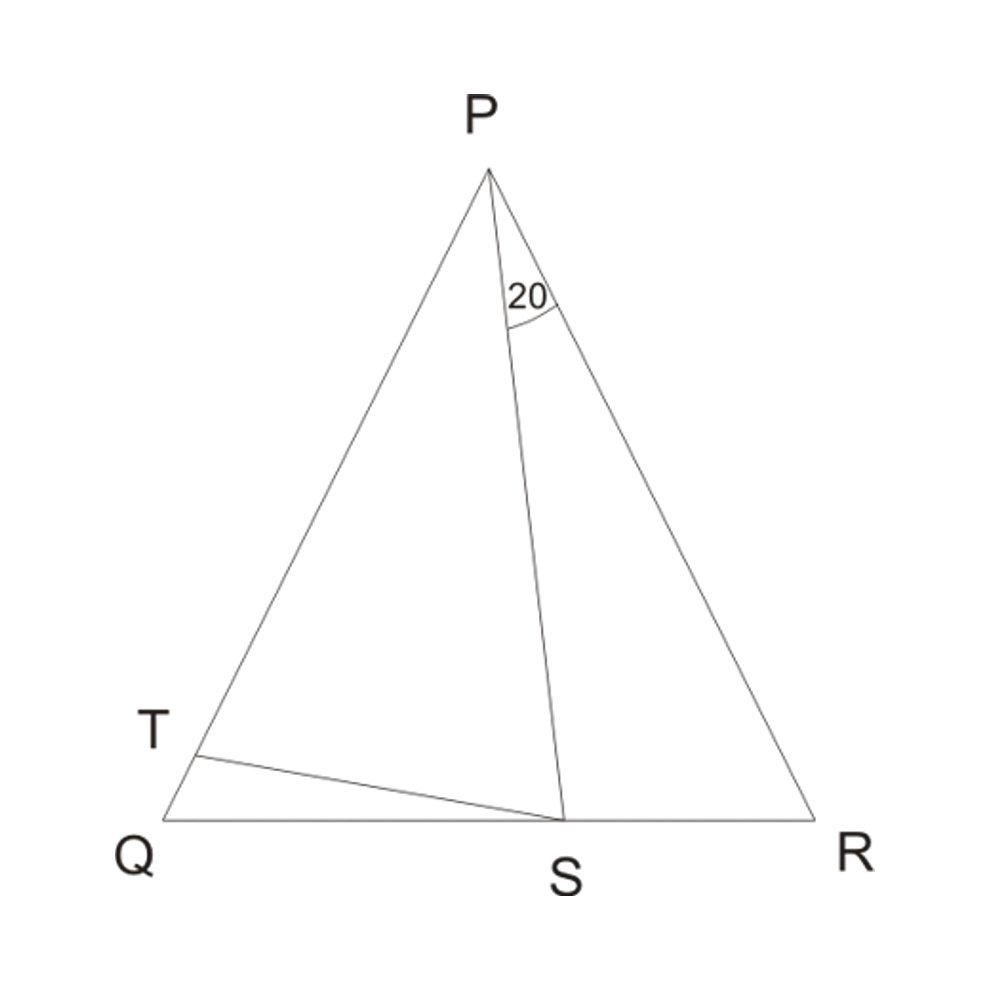
A △PQR\triangle PQR is an isosceles triangle where PQ=PRPQ=PR. point TT and SS is in PQPQ and QRQR respectively, so that △PTS\triangle PTS is an isosceles triangle with PT=PSPT=PS. if ∠RPS\angle RPS is 20∘20^\circ, Find ∠TSQ\angle TSQ?

#MathProblem #Math

Note by Ian Mana
8 years ago

No vote yet
4 votes

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

Let ∠TPS= x ,∠PTS=PST=z ,∠PQR=∠PRQ=y.

Thus we have,

2y=180-(20+x), or y= 180−(20+x)2\frac{180-(20+x)}{2}.

Again, 2z=(180-x). or, Z= (180−x)2\frac{(180-x)}{2}.

Now in △TQS, we have, ∠STP the external angle. Thus, z= y+ ∠TSQ or, ∠TSQ=(180−x)2\frac {(180-x)}{2}- 180−(20+x)2\frac{180-(20+x)}{2} or, ∠TSQ= 10

Bodhisatwa Nandi - 8 years ago

10 degrees.

let angle PRQ = angle PQR = x

angle PTS = x + angle TSQ

=> angle PST = x + angle TSQ

angle PSQ = angle PST + angle TSQ = x + 2 * angle TSQ angle PSQ = x + 20 (ext angle of triangle PSR)

=> 2 * angle TSQ = 20 => angle TSQ = 10

Ethan Tan - 8 years ago

Log in to reply

In your fifth line I get lost, you say x + 2 * angle TSQ angle PSQ. What does it mean?

Jordi Bosch - 8 years ago

∠PRQ = ∠PQR = a , because isosceles triangle.

∠PTS = ∠PST = b , because isosceles triangle.

∠TSQ = c

∠PSR = 180-(20+a) , because angles in a triangle add up to 180. Or, ∠PSR = 180-(b+c) , because angles in a straight line is 180.

Therefore we get 180-(20+a) = 180-(b+c), or simply, 20+a = b+c. Or in terms of a we get: a = b+c-20

∠QTS = 180-(a+c) . Or, ∠QTS = 180-b . Therefore we get a+c=b . Or in terms of a we get : a = b-c .

We now have two equations, (1) a = b+c-20 and (2) a = b-c

So, b+c-20 = b-c (Subtract b from both sides) c-20 = -c (Add c to both sides) 2c-20 = 0 Therefore, 2c = 20 or simply c = 10

The question asks for ∠TSQ which we named c. We found out c is 10 degrees. So answer is 10.

Mohammad Al Ali - 8 years ago
×

Problem Loading...

Note Loading...

Set Loading...