Its a tunnel in a planet

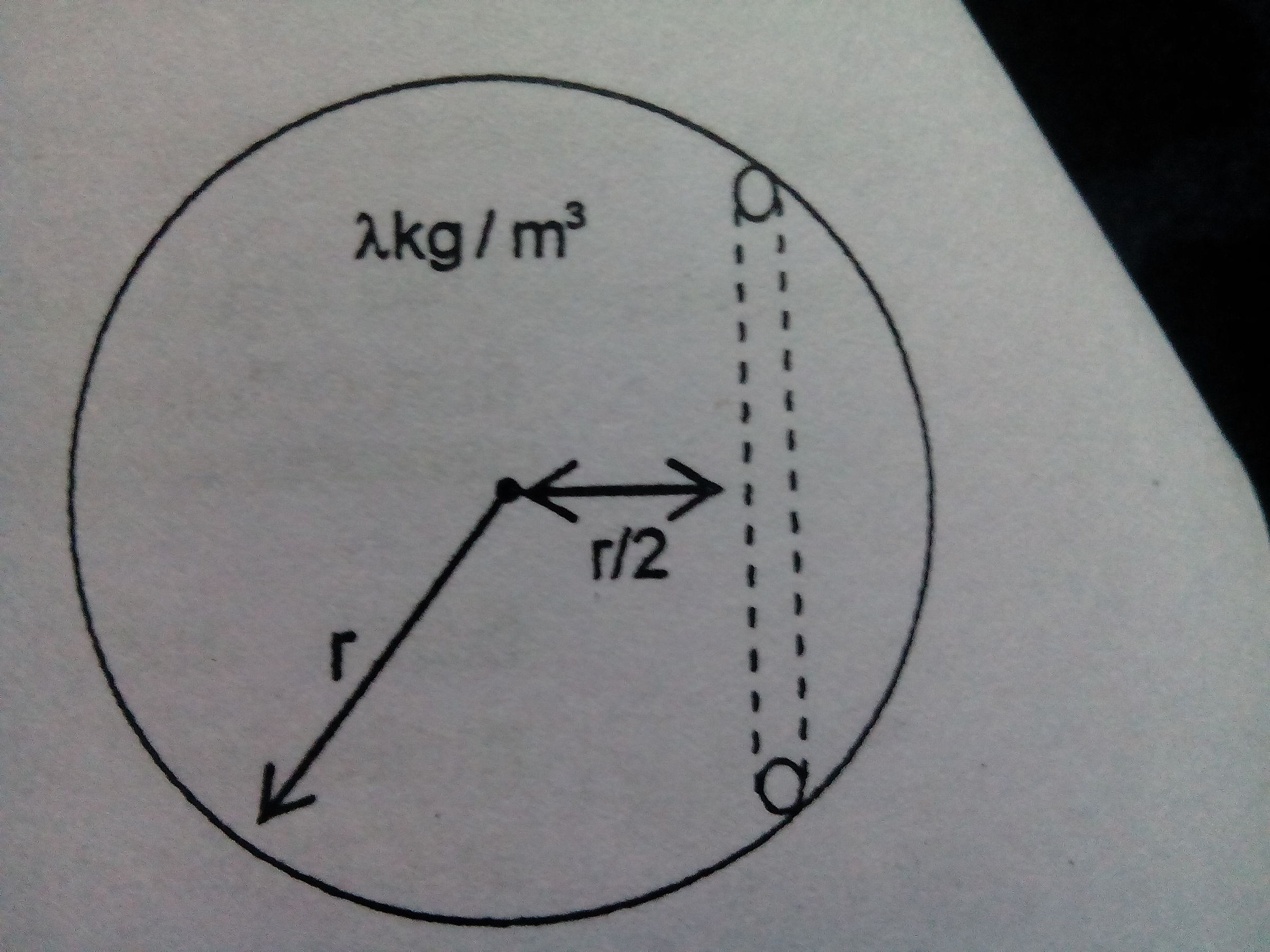
Consider a planet of radius $r$ having density $\lambda$ .A tunnel is dig inside it it at a distance $\frac{r}{2}$ from its centre as shown. An object of mass m is left in the tunnel at the surface at $t=0$

Find the time taken by the object to reach the mid of the tunnel and the normal reaction applied by wall of the tunnel on the object.

#Mechanics

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Hint, it doesn't matter how far the tunnel is from the center of the Earth.

Josh Silverman Staff - 6 years, 2 months ago

@Ronak Agarwal @Azhaghu Roopesh M @Rohit Shah @Krishna Sharma

Tanishq Varshney - 6 years, 2 months ago

How much are you getting in AIITS-8.

@Tanish

Ronak Agarwal - 6 years, 2 months ago

The answer key webpage is showing error so i couldn't match my answers

Tanishq Varshney - 6 years, 2 months ago

I totally messed up with the paper.

Prakhar Gupta - 6 years, 2 months ago

@Abhineet Nayyar @Kushal Patankar

Tanishq Varshney - 6 years, 2 months ago

@Tanishq Varshney

Use dimensional analysis(during exam).

The actual way is to use restoring force and stuff, with it you will get that the motion of the object in the tunnel is S.H.M.

Raghav Vaidyanathan - 6 years, 2 months ago

I want that stuff @Raghav Vaidyanathan

Tanishq Varshney - 6 years, 2 months ago

Hi Raghav

I need your view on this problem

Kushal Patankar - 6 years, 2 months ago

First of all, thanks for mentioning me @Tanishq Varshney !! Is the answer for time period = $\frac { \pi }{ 2 } \sqrt { \frac { 3 }{ 4\pi \lambda G } }$ ???

A Former Brilliant Member - 6 years, 2 months ago

I have same guess.

Kushal Patankar - 6 years, 2 months ago

Can u provide a hint or some expression to get the answer

Tanishq Varshney - 6 years, 2 months ago

@Tanishq Varshney – Since the motion inside is SHM , we know that force at amplitude is $F=A \omega^2$ here A= √3r/2 and you know what F is. You will get \omega there. And the rest is piece of cake.

Kushal Patankar - 6 years, 2 months ago

@Tanishq Varshney – See, first of all, i found the restoring force, in this case, a component of the gravitational force between the Earth and the object.

Tunnel In a Planet

Let's consider that the object starts from the centre and moves towards the surface. Consider a very small displacement $'x'$ from the centre such that the restoring force remains constant. Now, the motion of the body through this $'x'$ is an SHM which i will prove later. According to shell theorem, the Earth around this motion won't apply any force. So, the force is applied by a small sphere with radius $R=\sqrt { \frac { { r }^{ 2 } }{ 2 } +{ x }^{ 2 } }$ which is equal to $\frac { Gm\frac { 4 }{ 3 } \pi \lambda { R }^{ 3 } }{ { R }^{ 2 } }$ . But the restoring force will be the vertical component of this force = $\frac { G(\frac { 4 }{ 3 } \pi { R }^{ 3 }\lambda )m }{ { R }^{ 2 } } \frac { x }{ R }$ = $G\frac { 4 }{ 3 } \pi \lambda m(x)$

Clearly this force is directly proportional to $x$ and so, the motion is a simple harmonic one. So, the spring factor in the case is = $G\frac { 4 }{ 3 } \pi \lambda m$ and the time period is given by = $2\pi \sqrt { \frac { Mass\quad factor }{ Spring\quad factor } }$ = $2\pi \sqrt { \frac { m }{ \frac { 4 }{ 3 } \pi \lambda Gm } } =2\pi \sqrt { \frac { 3 }{ 4\pi \lambda G } }$

But since, you have asked about the time to move from extreme to mean, it is equal to $Time period/4$ = $\frac { \pi }{ 2 } \sqrt { \frac { 3 }{ 4\pi \lambda G } }$

And the normal reaction (I guess :P) will be given by the other component of the attractive force = $\frac { Gm\frac { 4 }{ 3 } \pi \lambda { R }^{ 3 } }{ { R }^{ 2 } } (\frac { r/2 }{ R } )\quad =\quad \frac { 2 }{ 3 } Gm\pi \lambda r$

So, how did i do?? Lol:D

A Former Brilliant Member - 6 years, 2 months ago

@A Former Brilliant Member – Thats it.

Kushal Patankar - 6 years, 2 months ago

@Kushal Patankar – Yayy! lol

A Former Brilliant Member - 6 years, 2 months ago

Can I have your views over here

Kushal Patankar - 6 years, 2 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$