just trying to make my first discussion :D and try to solve :D
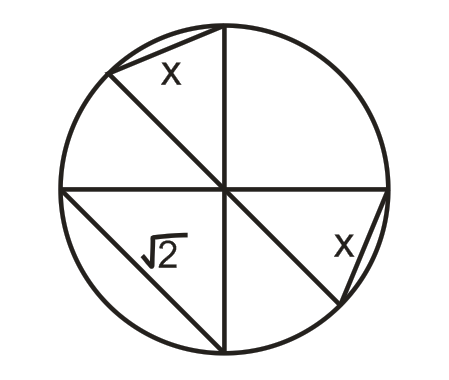
Three distinct diameters are drawn on a unit circle such that chords are drawn as shown in the figure. If the length of one chord is units and the other two chords are of equal lengths, what is the common length of these chords?
No vote yet
10 votes
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
since radius is 1(unit circle). the angle opposite to the Root 2 side is 90 (converse of pythagoras theorem. hence its vertically opposite angle is also 90.
calling the centre as o and the diameter on which the 2 equal sides sit on as AB.one side as AC and the other equal side as BD since the radii are equal and AC=BD from sss postulate angle BOD = angle AOC Since they are on a straight line with one angle as 90 degrees angle AOC=angle bod=45
then use cosine rule to get the answer
sqrt [ 2 - (sqrt 2) ]
root of 2-root 2
sorry didnt have time to put in latex
Log in to reply
nice can you explain how did you get it :D
Log in to reply
easy thing ans- sqrt[2-sqrt(2)]
Log in to reply
He said to explain.
(2−2)
I like this :]
We have a isosceles triangle whit a=x b=1 and angle at A is 45 (at B and C are 67.5 ) so we can make a right triangle witch has hypotenuse 1 and a side x/2. Since we have all the angles we can see that x/2 = 1cos(67.5) so x=2cos(67.5) or x=2*sin(22.5) witch is approximately 0.765
\sqrt (2- \sqrt 2)
Sweet....
sqrt(2-sqrt(2)). solved using basic geometry no trigonometry.