Kelongs (SPM Additional Mathematics 2019)
Solution by scale drawing is not accepted.
Diagram 3 shows the positions of jetty and kelongs , , , , and in the sea.
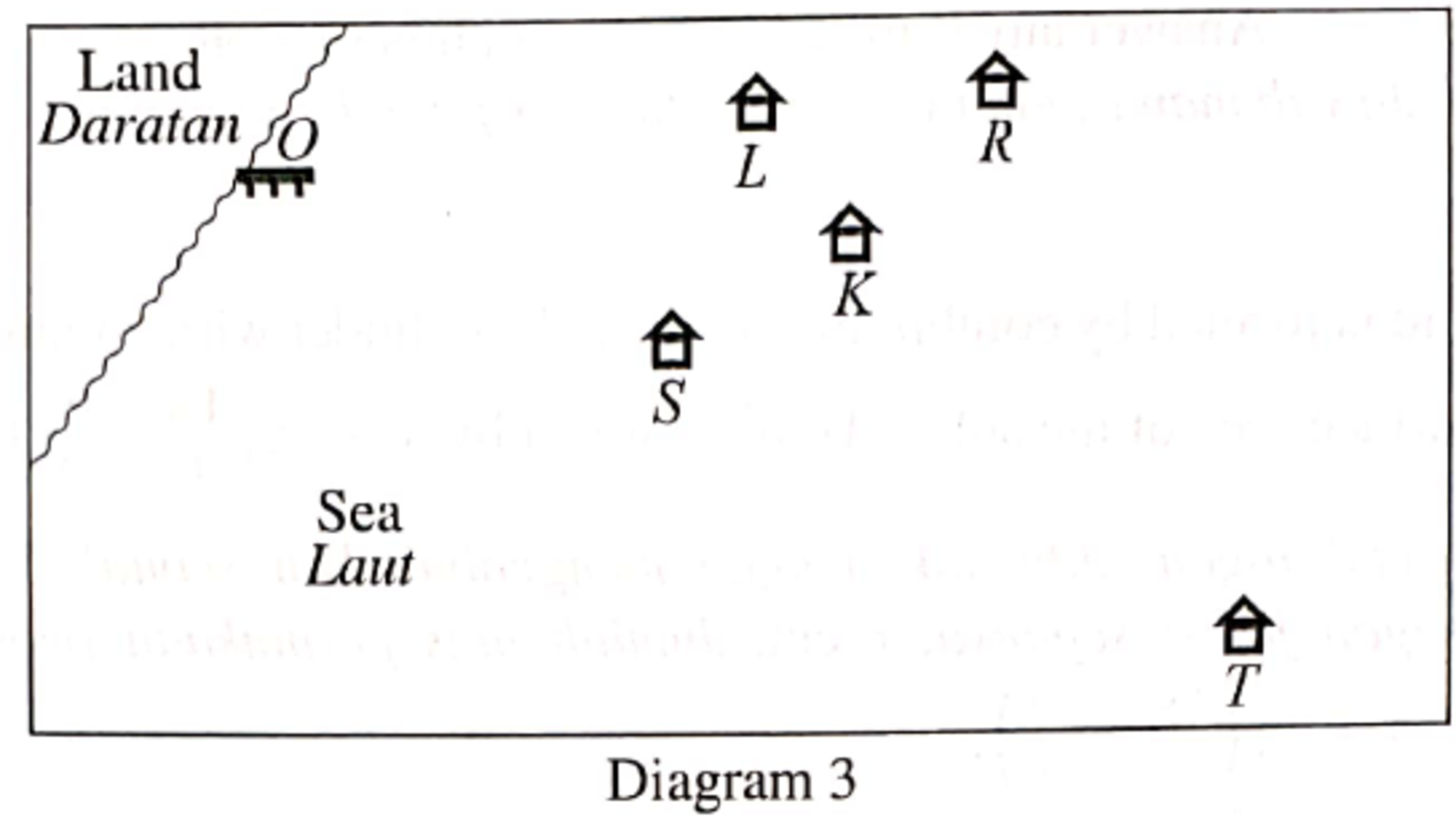 Kelong is situated from jetty and kelong is situated from jetty in the direction of . Kelong is situated from jetty and kelong is situated from kelong in the direction of . Kelongs , , and are situated on a straight line such that the distance of kelong from kelong is times its distance from kelong .
Kelong is situated from jetty and kelong is situated from jetty in the direction of . Kelong is situated from jetty and kelong is situated from kelong in the direction of . Kelongs , , and are situated on a straight line such that the distance of kelong from kelong is times its distance from kelong .
If Joe uses a pair of binoculars to observe kelong from kelong , determine whether kelong can be seen without being blocked by kelong or otherwise.
Prove your answer mathematically.
I tried to answer this question by using vectors and deciding whether the vectors and are collinear with vector or not. From my calculations, it seems that the answer should be that kelong can be seen from kelong without being blocked by kelong , but I'm not sure whether my answer is right or wrong.
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
Menelaus’s Theorem will give you the answer. K would block the view if distance of kelong K from kelong T was 3 times its distance from kelong LL instead of 5 times.