LC Impedance Conventions

It is fairly easy to derive AC impedance conventions for inductors and capacitors, starting with time-domain equations.

For the inductor:

$v(t) = L \frac{d}{dt} i(t)$

Take the Laplace transform:

$V(s) = L s I(s)$

Substituting in $s = j \omega$ .

$\frac{V(j \omega)}{I(j \omega)} = Z_L = j \omega L$

For the capacitor:

$i(t) = C \frac{d}{dt} v(t)$

Take the Laplace transform:

$I(s) = C s V(s)$

Substituting in $s = j \omega$ .

$\frac{V(j \omega)}{I(j \omega)} = Z_C = \frac{1}{j \omega C} = - \frac{j}{\omega C}$

This shows why inductors have $+ j$ impedance and capacitors have $- j$ impedance

Another way to show it is to examine the test signal $\sin(\omega t)$ . Suppose that this is the expression for the inductor current:

$i(t) = \sin(\omega t) \\ v(t) = L \frac{d}{dt} i(t) = \omega L \cos (\omega t)$

We can see that for the inductor, the voltage is greater than the current by a factor $\omega L$ , and it leads by 90 degrees (agreeing with the $+ j$ ) term derived earlier.

Now examine the capacitor in the time domain:

$v(t) = \sin(\omega t) \\ i(t) = C \frac{d}{dt} v(t) = \omega C \cos (\omega t)$

We see that the voltage is smaller than the current by a factor $\omega C$ , and that the voltage lags the current by 90 degrees, agreeing with the transfer function derived earlier.

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

@Steven Chase Thanks.

Talulah Riley - 9 months, 2 weeks ago

@Steven Chase is there any other way to prove it, other than laplace transform.

I have added a bit to the end

Steven Chase - 9 months, 2 weeks ago

@Steven Chase Yeah Thanks.

Your knowledge of Alternating current is next level.
I feel very unconfident while solving Alternating current problems.

@Steven Chase Therefore i have started series of Alternating current problems.
Make sure to drop a solution.
Hope I am not disturbing you.
Thanks in advance.

@Steven Chase https://brilliant.org/problems/alternating-current-series-4/

I'm not sure what the physical mechanism for that one is supposed to be. Do you have an idea?

@Steven Chase Yeah right now I got a YouTube channel where this problem is discussed.
Here is the video.

Talulah Riley - 9 months, 1 week ago

@Steven Chase Hello, Good Morning.
I have posted a new problem. Please check my answer is correct or not?
Thanks in advance.

@Steven Chase https://brilliant.org/problems/electromagnetic-induction-4/

@Steven Chase Good. Evening,Help me in this

@Steven Chase hello Good Afternoon,Try this problem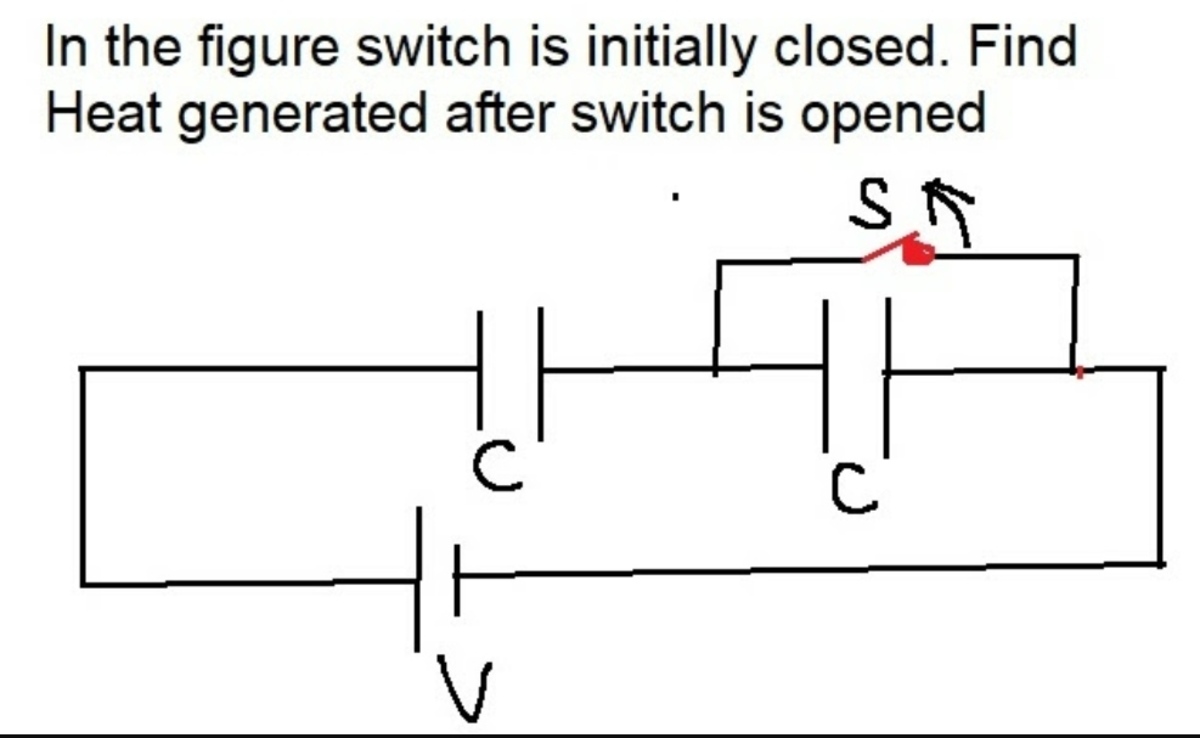
And share your views.

Initially, the left capacitor has voltage V and the right capacitor has no voltage. Then after the switch opens, the system is subject to the following constraints.

1) The sum of the two capacitor voltages must be V
2) Since the capacitors are in series, and they have the same capacitance, the change in one capacitor's voltage must exactly match the change in the other capacitor's voltage.

There are three scenarios to consider then:

1) The capacitor voltages are exactly the same after switch opening as before switch opening
2) Both capacitors increase their voltages relative to before switch opening
3) Both capacitors decrease their voltages relative to before switch opening

Scenarios 2 and 3 can't happen without violating constraint #1. Therefore nothing happens, and no heat is dissipated.

Steven Chase - 9 months, 1 week ago

@Steven Chase Your answer is correct but one thing which I have not understand properly is
“The capacitor voltages are exactly the same after switch opening as before switch opening”

@Talulah Riley – In other words, they don't change at all

@Steven Chase do you have edited the note?

Talulah Riley - 8 months, 3 weeks ago

It is the same as it was earlier

Steven Chase - 8 months, 3 weeks ago

@Steven Chase You have very much knowledge of electrical engineering.
Nowadays I am feeling jealous with you. :)

@Talulah Riley – No worries. I have been doing this a long time

@Steven Chase – @Steven Chase I was joking :). Just to make you feel better :)

@Steven Chase – @Steven Chase Do you mean that, you are making people feel jealous from long time ??

@Talulah Riley – No, I've been studying electrical engineering for a long time

@Steven Chase – @Steven Chase I know that, I was kidding you.

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$