Linear Algebra - Vector Spaces Quiz 6 (Least Squares) - Jeff Folster

In the least squares problem we find that

\[ A^T Ax = A^T b \]

and

$c_1 = \frac{\sum y_i}{n} , c_2 = \frac{\sum x_i y_i }{\sum x_i^2}$

where $y = c_1 + c_2 x$

I'm assuming this linear equation represents some kind of fitted line for the data. However, a previous step in the quiz involved setting all the $x_i$ coordinates to $x_i - \bar{x}$ to simplify finding $c_1$ and $c_2$ .

So I went ahead and tried this method on a simple set I made up of 20 pieces of data of coordinates $(x,y)$ :

$\{ (1,4), (3,5) , (4,3), (4,9), (6,2), (6,8), (8,6), (10,9), (11,7), (12, 5), (13,11), (14,7), (15,9), (16,12), (17,8), (18,10), (18,13), (19,14), (20,13), (20,14)\}$

A little spread out but I expect basically a positive linear relationship with y as a function of x.

Now I find with my calculator stat functions that $\bar{x} = 11.75$ , so I set all $x_i$ to $x_i - 11.75$ :

$X = \{ -10.75, -8.75, -7.75, -7.75, -5.75, -3.75, -1.75, -0.75, 0.25, 1.25, 2.25, 3.25, 4.25, 5.25, 6.25, 6.25, 7.25, 8.25, 8.25 \}$

My calculations from here:

$c_1 = \frac{\sum y_i}{n} = \frac{169}{20} = 8.45$ $c_2 = \frac{\sum x_i y_i}{\sum x_i^2} = \frac{340.25}{725.75} \approx 0.46883$

I wind up with a line equation that looks like

$y = 0.46883x + 8.45$

If I try and plot this, the line sits way outside any of my data.

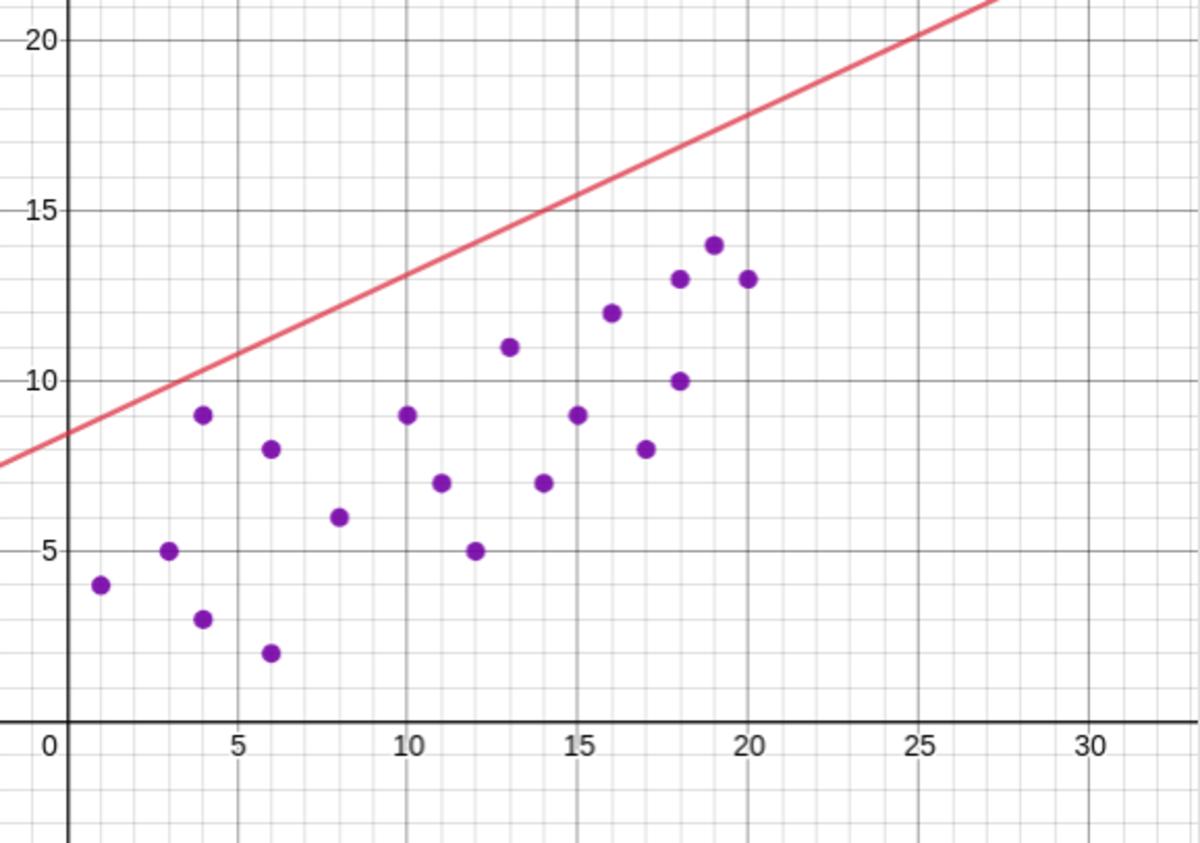
Did I miss some crucial step? Do the two constants change in subtracting the mean of X to begin with? Or am I misunderstanding the meaning of $c_1$ and $c_2$ ? As far as I can tell the quiz doesn't seem to suggest one way or another.

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

There are no comments in this discussion.

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$