Luscious Integration

Here is a problem I=∫1(16+9sin⁡x)2dx I=\int \frac{1}{(16+9 \sin x) ^{2}}dx
Here is the solution
+C\large +C

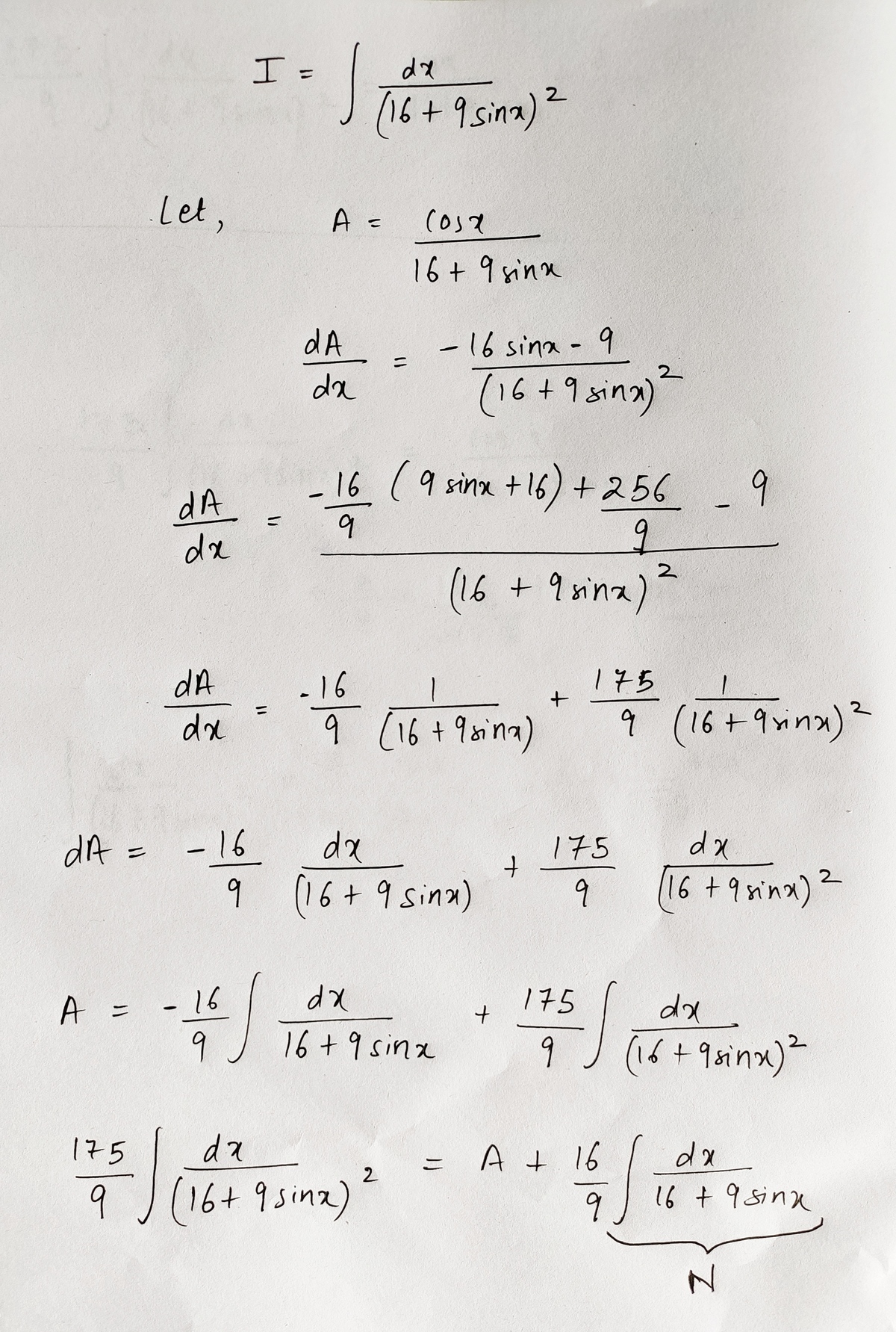
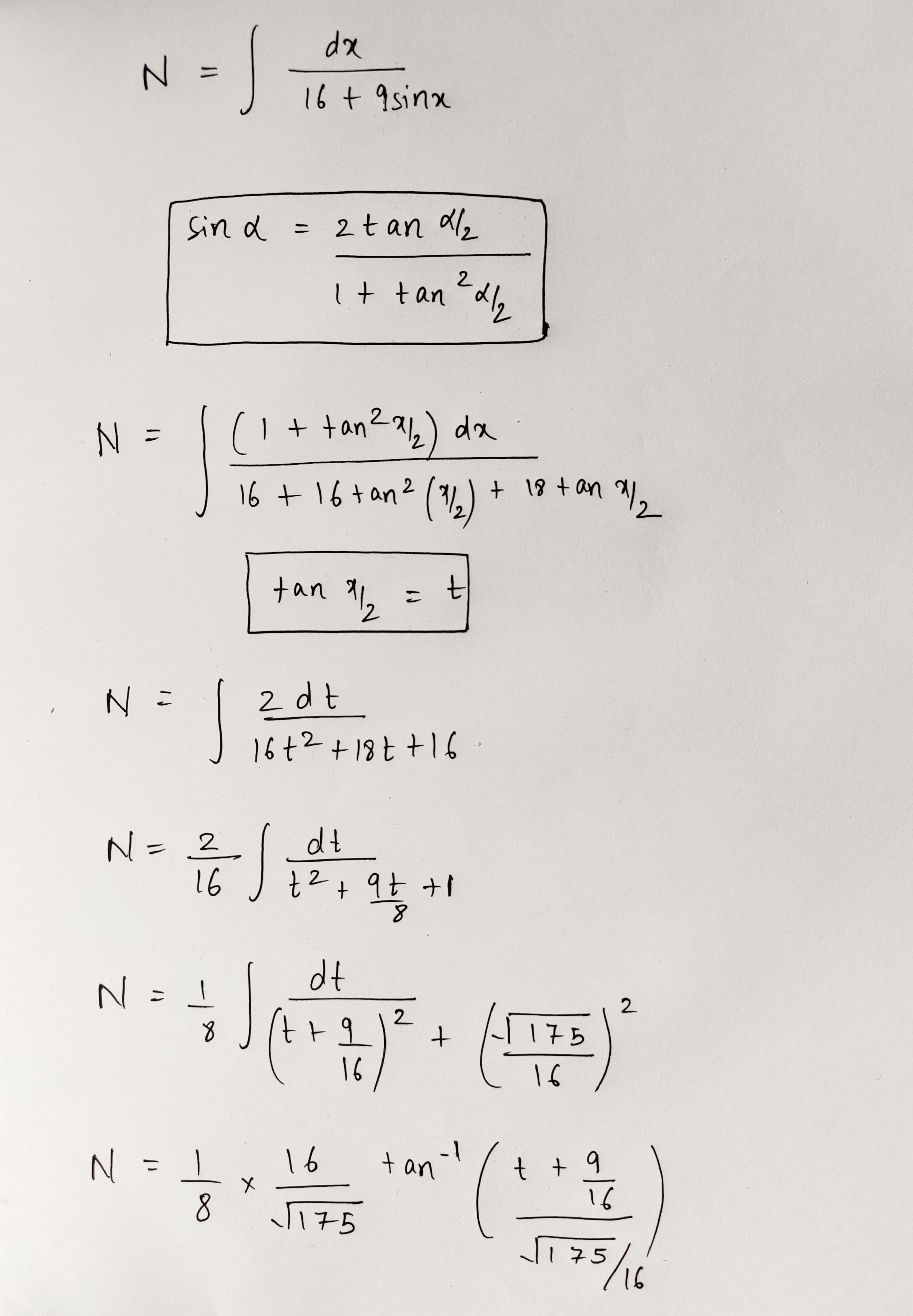
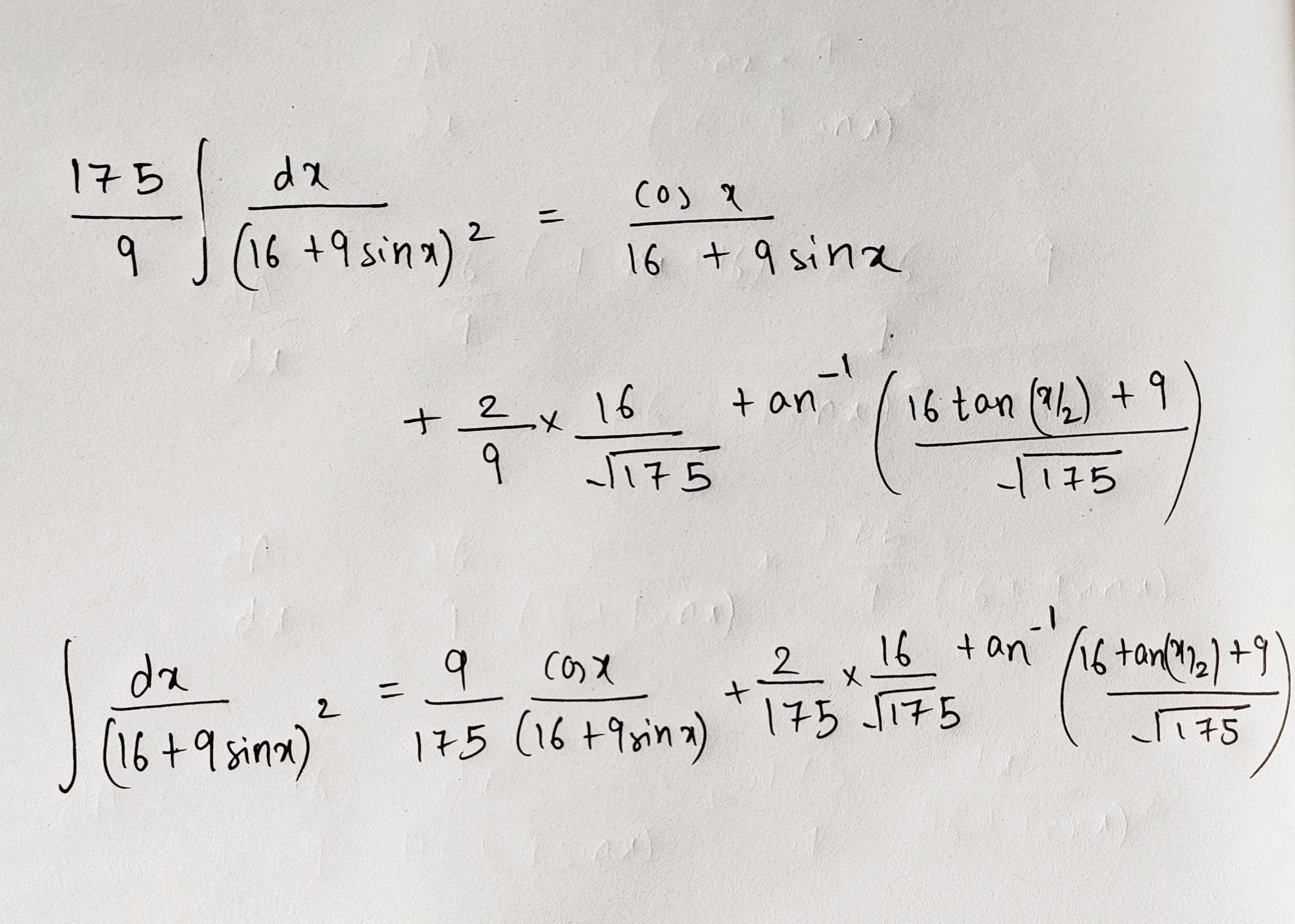
Feel fee to ask anything regarding my solution.

#Calculus

Note by Talulah Riley
9 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

Here's an alternative approach.

Let y=π2−xy = \frac\pi2 - x. Then, the integral becomes I=−∫dy(16+9cos⁡y)2\displaystyle I = -\int \dfrac{dy}{(16 + 9\cos y)^2} .

Using half angle tangent substitution, we have t=tan⁡(y2),cos⁡y=1−t21+t2t = \tan(\frac y2) , \cos y = \dfrac{1-t^2}{1+t^2} and dy=2⋅dt1+t2dy = \dfrac{2 \cdot dt}{1 + t^2} . The integral transforms to

I=−2∫1(16+9(1−t21+t2))2⋅11+t2 dt0=−2∫1+t2(16(1+t2)+9(1−t2))2 dt0=−2∫t2+1(7t2+25)2 dt0=−27∫7t2+7(7t2+25)2 dt0=−27∫7t2+25−18(7t2+25)2 dt0=−27∫17t2+25 dt+367∫1(7t2+25)2 dt0\begin{array} { r c l} I &=& \displaystyle -2 \int\dfrac1{\left (16 + 9 \left(\frac{1-t^2}{1+t^2} \right)\right)^2} \cdot \dfrac1{1+t^2} \, dt \\\phantom 0 \\ &=& \displaystyle -2 \int \dfrac{1+t^2}{ (16(1+t^2) + 9(1-t^2) )^2} \, dt \\ \phantom 0 \\ &=& \displaystyle -2 \int \dfrac{t^2 + 1}{ (7t^2 + 25 )^2} \, dt \\ \phantom0 \\ &=& \displaystyle -\frac27 \int \dfrac{7t^2 + 7}{ (7t^2 + 25 )^2} \, dt \\ \phantom0 \\ &=& \displaystyle -\frac27 \int \dfrac{7t^2 + 25 - 18}{ (7t^2 + 25 )^2} \, dt \\ \phantom0 \\ &=& \displaystyle -\frac27 \int \dfrac1{ 7t^2 + 25 } \, dt + \dfrac{36}{7} \int \dfrac1{(7t^2 + 25)^2} \, dt \\ \phantom0 \\ \end{array}

For both integrals, apply the trigonometric substitution, 7t=5tan⁡u⇒7=5sec⁡2u⋅dudt\sqrt7 t = 5 \tan u \Rightarrow \sqrt7 = 5\sec^2 u \cdot \dfrac{du}{dt} .

I=−27∫125sec⁡2u⋅57sec⁡2u du+367∫1(25sec⁡2u)2⋅57sec⁡2u du0=−2357∫du+368757∫cos⁡2u du0=−2357u+368757⋅14(sin⁡(2u)+2u)+C0=−328757u+98757sin⁡(2u)+C0 \begin{array} {r c l} I &=& \displaystyle -\frac27 \int \dfrac1{25\sec^2 u} \cdot \dfrac5{\sqrt7} \sec^2 u \, du + \dfrac{36}{7} \int \dfrac1{(25\sec^2 u)^2} \cdot \dfrac5{\sqrt7} \sec^2 u \, du \\ \phantom 0 \\ &=& \displaystyle -\frac2{35\sqrt7} \int du + \dfrac{36}{875\sqrt7} \int \cos^2 u \, du \\ \phantom 0 \\ &=& \displaystyle -\frac2{35\sqrt7} u + \dfrac{36}{875\sqrt7} \cdot \frac14 (\sin(2u) + 2u) +C \\ \phantom 0 \\ &=& \displaystyle -\frac{32}{875\sqrt7} u + \dfrac{9}{875\sqrt7} \sin(2u) + C \\ \phantom 0 \\ \end{array}

What's left is to back-substitute. u=tan⁡−1(75t)=tan⁡−1(75tan⁡(y2))=tan⁡−1(75tan⁡(π/2−x2))u = \tan^{-1} \left( \frac{\sqrt7}5 t\right)= \tan^{-1} \left( \frac{\sqrt7}5 \tan\left( \frac y2\right)\right)= \tan^{-1} \left( \frac{\sqrt7}5 \tan\left( \frac {\pi /2 - x}2\right)\right) . Finishing it off with tan⁡(π/2−x2)=1−tan⁡(x2)1+tan⁡(x2) \tan\left( \frac {\pi /2 - x}2\right) = \dfrac{1 - \tan(\frac x2)}{1 + \tan(\frac x2)} , we get:

I=−328757tan⁡−1(75tan⁡(1−tan⁡(x2)1+tan⁡(x2)))+98757sin⁡[2(tan⁡−1(75tan⁡(1−tan⁡(x2)1+tan⁡(x2))))]+C I = \displaystyle -\frac{32}{875\sqrt7} \tan^{-1} \left( \frac{\sqrt7}5 \tan\left( \dfrac{1 - \tan(\frac x2)}{1 + \tan(\frac x2)} \right)\right) + \dfrac{9}{875\sqrt7} \sin \left [ 2\left( \tan^{-1} \left( \frac{\sqrt7}5 \tan\left( \dfrac{1 - \tan(\frac x2)}{1 + \tan(\frac x2)} \right)\right) \right) \right] + C

Pi Han Goh - 9 months ago

Log in to reply

@Pi Han Goh very very nice. Thanks for sharing.
By the way, do you know I am Neeraj . Due to some reason I have changed my name

Talulah Riley - 9 months ago

Log in to reply

Now I know.

Pi Han Goh - 9 months ago

Log in to reply

@Pi Han Goh – @Pi Han Goh your integration skills are very nice.

Talulah Riley - 9 months ago

@Pi Han Goh

Nice one. I like it.

Krishna Karthik - 9 months ago

@Pi Han Goh Btw have you ever participated in an Integration bee or an Integration competition? Holy shit... you're really good!

Krishna Karthik - 9 months ago

Log in to reply

No, but I'm aware of these competitions.

Pi Han Goh - 9 months ago

Log in to reply

@Pi Han Goh – @Pi Han Goh how to solve this integration, is there any alternative methods also? , ∫π2π(x2+2)cos⁡xx3dx\int_{π}^{2π} \frac{(x^{2}+2) \cos x}{x^{3}} dx
Thanks in advance

Talulah Riley - 9 months ago

Log in to reply

@Talulah Riley – Try posting each distinct question in a different note. Otherwise, it gets really cluttered and messy to see what note is.

Pi Han Goh - 9 months ago

Log in to reply

@Pi Han Goh – @Pi Han Goh ok, I will post a note after one hour.

Talulah Riley - 9 months ago

@Pi Han Goh I have upvoted your solution here also, see above.

Talulah Riley - 8 months, 3 weeks ago

@Krishna Karthik Here it is, I'm going to bed now.

Talulah Riley - 9 months ago

@Steven Chase @Karan Chatrath , in case you guys are interested.

Talulah Riley - 9 months ago

Log in to reply

Yeah; it's really impressive. Good job mate :)

Krishna Karthik - 9 months ago

Here's another method:

The integrand can be expressed as 1+9cos⁡x−9cos⁡x(16+9sin⁡x)2=1+9cos⁡x(16+9sin⁡x)2−9sin⁡x(16+9sin⁡x)2. \dfrac{1 + 9\cos x - 9\cos x}{(16 + 9\sin x)^2} = \dfrac{1 + 9\cos x}{(16 + 9\sin x)^2} - \dfrac{9\sin x}{(16 + 9\sin x)^2}.

Split this into two integrals, for the first integral, let y=π2−xy = \frac \pi2 - x then t=tan⁡(y2)t = \tan(\frac y2) , and you can solve it like how I've written in my other comment. And use u=16+9sin⁡xu = 16 + 9\sin x to solve the second integral.

Pi Han Goh - 9 months ago

Log in to reply

@Pi Han Goh Thank you so much

Talulah Riley - 9 months ago

Bruh that's fuggin awesome!!!!

Krishna Karthik - 9 months ago

Log in to reply

@Krishna Karthik Do you know above line?

Talulah Riley - 9 months ago

Log in to reply

Sorry? Yeah; you're going to bed. Cya.

Krishna Karthik - 9 months ago

Log in to reply

@Krishna Karthik – @Krishna Karthik it is the style of Steven Sir.

Talulah Riley - 9 months ago

Log in to reply

@Talulah Riley – Lol I just love how you added a funny little "plus C" at the end lmao

Krishna Karthik - 9 months ago

Log in to reply

@Krishna Karthik – @Krishna Karthik i forgot to write it in page. But this seems me more beautiful.
Conclusion:Everything happens for good

Talulah Riley - 9 months ago

@Pi Han Goh @Krishna Karthik can you please help me in this integration ∫π2π(x2+2)cos⁡xx3dx\int_{π}^{2π} \frac{(x^{2}+2) \cos x}{x^{3}} dx

Talulah Riley - 9 months ago

Log in to reply

@Lil Doug This one's actually quite easy. I'll post a solution soon.

Krishna Karthik - 9 months ago

Log in to reply

@Krishna Karthik please post it now.

Talulah Riley - 9 months ago

Log in to reply

@Talulah Riley – So, the integral can be rewritten as:

∫(cos⁡(x)x+2cos⁡(x)x3)dx\displaystyle \int \left( \frac{\cos(x)}{x} + \frac{2 \cos(x)}{x^3} \right) dx

So, we can split it into two integrals, which we can do using integration by parts.

∫cos⁡(x)xdx+2∫cos⁡(x)x3dx\displaystyle \int \frac{\cos(x)}{x} dx + 2 \int \frac{\cos(x)}{x^3} dx

So, we do integration by parts with the first half:

u=1x\displaystyle u = \frac{1}{x}, dv=cos⁡(x)\displaystyle dv = \cos(x)

du=−1x2\displaystyle du = - \frac{1}{x^2}, v=sin⁡(x)\displaystyle v = \sin(x)

So, it can be rewritten as:

I1=sin⁡(x)x−∫sin⁡(x)x2\displaystyle I_1 = \frac{\sin(x)}{x} - \int \frac{\sin(x)}{x^2}

Doing integration by parts for the second half, we get:

I2=−cos⁡(x)2x2−∫sin⁡(x)x2\displaystyle I_2 = - \frac{\cos(x)}{2x^2} - \int \frac{\sin(x)}{x^2}

Now simplifying, ∫sin⁡(x)x2\displaystyle \int \frac{\sin(x)}{x^2} cancels out, leaving:

xsin⁡(x)−cos⁡(x)x2+C\displaystyle \frac{x \sin(x) - \cos(x)}{x^2} + C

So substituting, you get:

−54π2\displaystyle \boxed{ \frac{-5}{4 \pi^2}}

Krishna Karthik - 9 months ago

Log in to reply

@Krishna Karthik – @Krishna Karthik how does it get cancel, both are negative, both will add up.

Talulah Riley - 9 months ago

Log in to reply

@Talulah Riley – Oh wait... shit. I fucked up. So, let's try to calculate that integral ∫sin⁡(x)x2\displaystyle \int \frac{\sin(x)}{x^2}

Krishna Karthik - 9 months ago

@Krishna Karthik what answer you are getting?

Talulah Riley - 9 months ago

Log in to reply

@Talulah Riley – I've posted the solution. It's just integration by parts.

Krishna Karthik - 9 months ago

I suspect the indefinite integral is in the form of A⋅sin⁡xx+B⋅sin⁡xx2+C⋅cos⁡xx+D⋅cos⁡xx2,A \cdot \dfrac{\sin x}x + B \cdot \dfrac{\sin x}{x^2} + C \cdot \dfrac{\cos x}{x} + D \cdot \dfrac{\cos x}{x^2}, where A,B,C,DA,B,C,D are constants. Differentiating this expression with respect to xx should gives us back the integrand (x2+2)cos⁡xx3 \dfrac{(x^2 + 2)\cos x}{x^3} .

Using quotient rule and comparing coefficients, we will get (A,B,C,D)=(1,0,0,−1)(A,B,C,D) = (1,0,0,-1) , thus ∫π2π(x2+2)cos⁡xx3 dx=[sin⁡xx−cos⁡xx2]π2π=−54π2≈−0.126651. \int_\pi^{2\pi} \dfrac{ (x^2+2)\cos x}{x^3} \, dx = \left [ \dfrac{\sin x}x - \dfrac{\cos x}{x^2} \right ]_{\pi}^{2\pi} = \boxed{-\dfrac{5}{4\pi^2} } \approx-0.126651 .

Pi Han Goh - 9 months ago

@Krishna Karthik i am getting I1=sin⁡xx+∫sin⁡xx2dxI_{1} =\frac{\sin x}{x}+\int \frac{\sin x }{x^{2}} dx

Talulah Riley - 9 months ago

Log in to reply

You missed out the −cos⁡(x)x2\displaystyle -\frac{\cos(x)}{x^2} term.

Krishna Karthik - 9 months ago

Log in to reply

@Krishna Karthik where bro, I am. Telling I1I_{1}

Talulah Riley - 9 months ago

Log in to reply

@Talulah Riley – Oh oops; my bad. Yup. I meant the exact same thing as you. So they should cancel!

Krishna Karthik - 9 months ago

@Talulah Riley – Wait... how are you getting a positive ∫sin⁡(x)x2\displaystyle \int \frac{\sin(x)}{x^2}? It should be negative because −1x2\displaystyle -\frac{1}{x^2}

Krishna Karthik - 9 months ago

Btw, numerically integrating, I'm getting -0.12779

Krishna Karthik - 9 months ago

Log in to reply

@Krishna Karthik share the code also.

Talulah Riley - 9 months ago

Log in to reply

@Talulah Riley – I'm just using a standard midpoint rule calculator through python.

Krishna Karthik - 9 months ago

Log in to reply

@Krishna Karthik – @Krishna Karthik share the code means share the code.

Talulah Riley - 9 months ago

Log in to reply

@Talulah Riley – Lmao, ok. Coming up.

Krishna Karthik - 9 months ago

@Lil Doug The code. 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import math

def function(x):
  return ((x**2+2)*math.cos(x))/x**3




n=2500

b=6.28

a=3.14


deltaX=(b-a)/n

def mean(a,b):
  meanValue=(a+b)/2
  return meanValue

xValue=[a]
heightValue=[]

for i in range(0,n):
  xValue.append(a+deltaX)
  deltaX=deltaX+(b-a)/n

for i in xValue:
  heightValue.append(function(mean(i,i+(b-a)/n)))
del heightValue[-1]


the_sum=sum(heightValue)
definite_integral=the_sum*((b-a)/n)

print('Definite integral evaluated by midpoint rule: '+str(definite_integral))

Krishna Karthik - 9 months ago

Log in to reply

Btw, you can shorten your code by doing this instead:

1
2
3
4
5
6
7
from math import cos, pi

def function(x): return ((x**2+2)* cos(x))/x**3

n = 2500 ; a = pi ; b = 2 * pi

# The rest is the same.

Pi Han Goh - 9 months ago

Log in to reply

@Pi Han Goh I don't like to code in single-line style. I prefer readability as a programmer, personally.

Usually, I prefer to indent functions so I can see what is inside the function clearer. And btw thx for the suggestion of using it as just cos and pi rather than specifying the library.

Krishna Karthik - 8 months, 3 weeks ago

Log in to reply

@Krishna Karthik – @Krishna Karthik No matter whatever you like, First upvote his alternative method of this note integration above.

Talulah Riley - 8 months, 3 weeks ago

Log in to reply

@Talulah Riley – @Lil Doug Oh yeah; sorry I forgot to. You can't upvote subcomments, though, sadly.

Krishna Karthik - 8 months, 3 weeks ago

@Krishna Karthik They are not cancelling bro
I think you have copied the solution and just paste it here.
Not taken a look on the solution

Talulah Riley - 9 months ago

Log in to reply

No, I looked. And you're right; they're not cancelling. My integration by parts has failed. We should work out ∫sin⁡(x)x2\displaystyle \int \frac{\sin(x)}{x^2}

Krishna Karthik - 9 months ago

Log in to reply

@Krishna Karthik it is not your integration by parts .
It is the mistake of this website https://www.integral-calculator.com/ who told you wrong method

Talulah Riley - 9 months ago

Log in to reply

@Talulah Riley – Integral calculator? I worked most of this out by hand; I tried integrating by parts. I checked with integral calculator because I got stuck midway; it mistakingly said it would cancel out (integral calculator can be stupid sometimes...) so I copied an integration by parts method from them. Maybe there's some weird trig substitution or something that I'm missing. I'll try the problem soon.

Krishna Karthik - 9 months ago

Log in to reply

@Krishna Karthik – @Krishna Karthik. you code is also not working

Talulah Riley - 9 months ago

Log in to reply

@Talulah Riley – It is. Show me your screen so I can debug for you.

Krishna Karthik - 9 months ago

Btw the my midpoint rule calculator seems to be coming up with a reasonable answer. This is actually a tricky problem... maybe integration by parts isn't the trick. Ask Pi Han Goh.

Krishna Karthik - 9 months ago

@Lil Doug I just posted a new note; it's a photo of the working code.

Krishna Karthik - 9 months ago

@Pi Han Goh here above you can see

Talulah Riley - 8 months, 1 week ago

Log in to reply

A few pointers:

  • Why start with A=⋯A = \cdots (yes, I know the answer to this question). But you seem to pull it out of thin air without any justification.

  • Say you used quotient rule, otherwise, the newbies can't follow this reasoning.

  • At least motivate why you want to work on the differentiation of AA first, by first explaining that the original integrand needs to be broken down (by considering a lesser power in the denominator).

  • Where did your sin⁡α=⋯\sin \alpha =\cdots come from ? (I know the answer to this question too) It seems mystifying to the uninitiated.

  • At least make it explicit why you want convert the integrand in the form of 1t2+a2 \frac1{t^2 + a^2} in the final step.

  • Handwriting issue: Some of your brackets does not properly encapsulate the required expressions.

  • Handwriting issue: Some of your fractions' horizontal line should be longer.

Pi Han Goh - 8 months, 1 week ago
×

Problem Loading...

Note Loading...

Set Loading...