M Sort - a new sorting algorithm

Introduction:

Most sorting algorithms have a predefined plan to sort a collection of objects, and they are often built to assume random input data. This has led them to do extra work than what is necessary and sometimes certain sequences of data slows down the sorting algorithm remarkably. Another consequence of this is that some sorting algorithms are known to perform well in certain conditions while others perform better in other circumstances. For instance, Quick Sort performs well in completely random data while it suffers with partially sorted data or with sorted collections. A good sorting algorithm should be designed to deal with any data and to do the minimum required steps to sort a collection and it should perform well under any circumstance.

After a while working with collections, I observed that each collection of objects consists of one or more sorted sublists (SSLs) of two or more elements in ascending or descending order, regardless of how the objects are positioned in the collection. The total number of elements in all SSLs is equal to the collection's size and the number of SSLs in a collection ranges from a minimum of one to a maximum of n/2. No matter how the elements are shuffled in a collection, the number of SSLs will always be between one and n/2, with one being the best case and n/2 as the worst case. So, for a collection of 10 elements, the minimum number of SSLs is one in the case of a sorted state and a maximum of five in the case of completely random data. The number of SSLs in a collection has an adverse relationship with how sorted the collection is. The more the number of SSLs a collection has, the more it is close to random data. And the fewer SSLs a collection has, the closer it is to a sorted state.

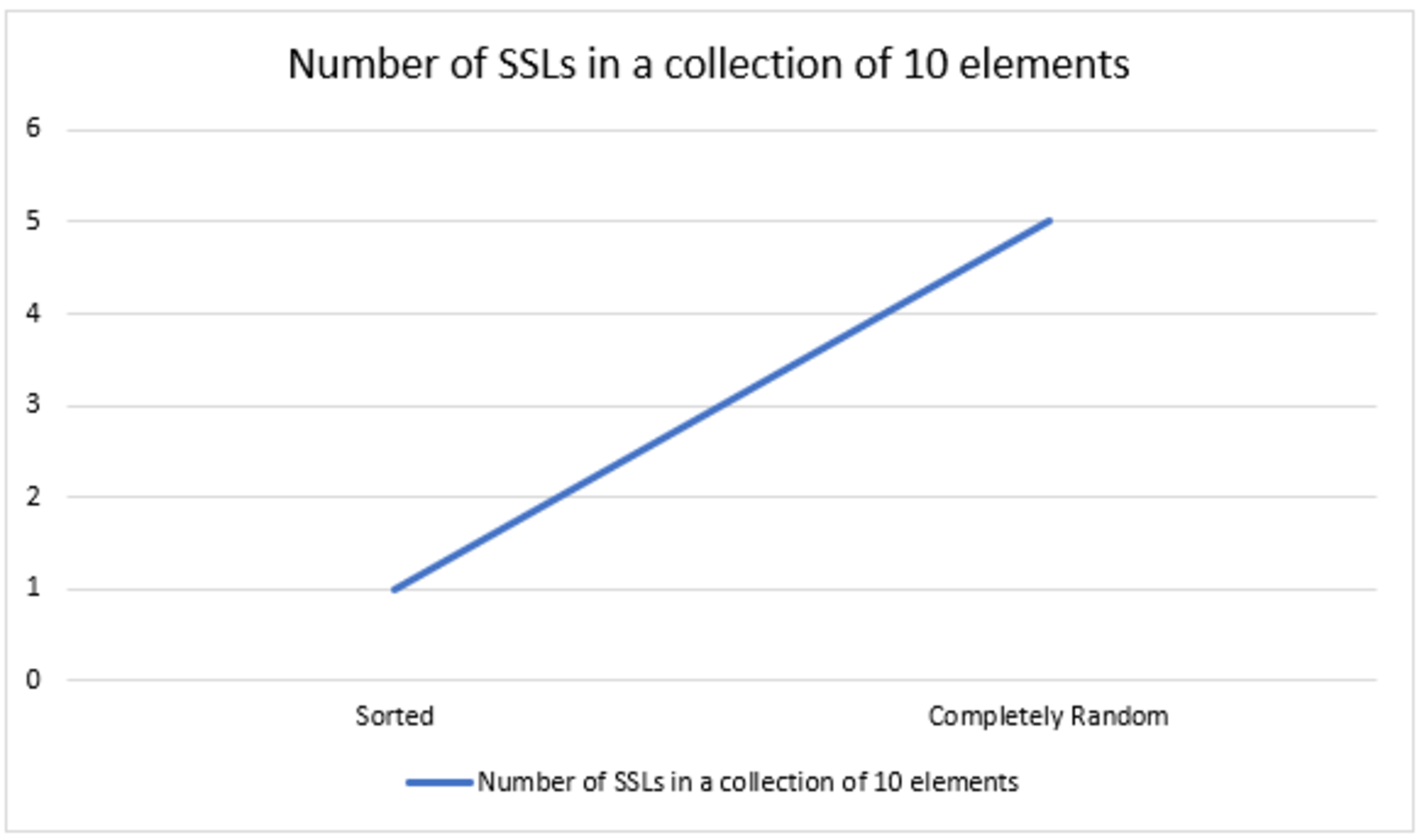
If we designed a sorting algorithm that gathers these SSLs and then merges them in one SSL, we will get a sorting algorithm that works in all scenarios and will always do the minimum work required to do the sorting, as the amount of work required is proportional to the number of SSLs in the collection, and here where M Sort comes in.

M Sort Design:

M Sort is a new sorting algorithm that works by gathering and merging SSLs present in a collection until we are left with one SSL and then the collection is sorted. It is implemented to have two main routines:

• Find SSLs: M Sort iterates through the array once to find SSLs.
• Merge: Next, it merges those SSLs until we are left with one SSL.

More on SSLs:

An SSL could be consisted of consecutive ascending or descending elements with the possibility of the presence of equal elements anywhere in the SSL, in the start, in the middle, or at the end. An ascending SSL could have equal elements in it and a descending SSL could have equal elements in it as well.

All the following are valid SSLs:

• Ascending with no equal elements: $\boxed{15, 25, 28, 33, 50, 100, 201, 300, 500, 505}$
• Ascending with equal elements $\boxed{15, 15, 15, 33, 50, 100, 201, 201, 500, 500}$
• Descending with no equal elements $\boxed{25, 20, 17, 16, 10, 9, 7, 5, 3, 1}$
• Descending with equal elements $\boxed{25, 25, 17, 16, 10, 10, 7, 5, 1, 1}$

Benefits of using this design:

Using such design yields many benefits:

• It always does the minimum steps required to sort a collection.
• It always performs well regardless of how the elements are positioned in the collection.
• It doesn’t need to check for special cases like sorted or reversed collections.
• It does not require random access to data, bidirectional access is enough as no jumping is required like Heap Sort or Shell Sort. It can be even tweaked to work with forwarding access only. This will make it possible for M Sort to be used with a wide variety of data structures like arrays, lists, or linked lists.

Implementation:

M Sort is implemented, in the code provided below, in one function to sort an array of integers. It simply finds SSLs and merges them into one SSL. There is no use of different sorting algorithms or fancy complex merging techniques, just a simple SSL finding routine, and a simple merging routine. Although it can be simply enhanced in performance or templatized, the goal here is to emphasize the idea M Sort tries to provide with simple to understand steps and not to provide a complex implementation.

// C++ Code
#include <iostream>
#include <algorithm>

using namespace std;

// Sorts an array of integers
void MSort(int* from, int* to)
{
    // Base case
    if (from >= to) return;

    // Struct to hold SSLs
    struct SSL
    {
        int* from;
        int* to;
        size_t size;
    };

    // Size of SSL array
    constexpr auto SSL_SZ = 100;

    // SSL array
    SSL ssl[SSL_SZ]{};

    // Used for merging
    SSL left, right;

    // SSL count
    int n = 0;

    // Size of array
    size_t size = to - from;

    // Allocate temp
    int* temp = new int[size - size / 2];

    // Check if temp was allocated
    if (temp == nullptr) 
    {
        throw "No memory for temp storage";
    }

    // Iterators
    int* ssl_from = from;
    int* ssl_to = from + 1;
    int* dest;

    // Iterate, find, add, and merge
    while (ssl_to < to)
    {
        // Find next SSL
        if (*ssl_to > *(ssl_to - 1))
        {
            for (++ssl_to; ssl_to < to && *ssl_to >= *(ssl_to - 1); ++ssl_to);
        }
        else if (*ssl_to < *(ssl_to - 1))
        {
            for (++ssl_to; ssl_to < to && *ssl_to <= *(ssl_to - 1); ++ssl_to);
            reverse(ssl_from, ssl_to);
        }
        else if (++ssl_to < to)
        {
            continue;
        }

        // Add SSL
        if (ssl_from < to && ssl_to >= ssl_from)
        {
            ssl[n].from = ssl_from;
            ssl[n].to = ssl_to;
            ssl[n].size = ssl_to - ssl_from;
            ++n;

            // Set next SSL start
            ssl_from = ssl_to;     

            // Add last SSL, if we reached the end
            if (++ssl_to >= to && ssl_from < to)
            {
                ssl[n].from = ssl_from;
                ssl[n].to = to;
                ssl[n].size = to - ssl_from;
                ++n;
            }
        }

        // Merge
        while (n > 1)
        {
            // SSLs to merge
            left = ssl[n - 2];
            right = ssl[n - 1];

            // Merge
            if (right.size >= left.size)
            {
                // Merge left                
                dest = left.from;
                left.to = copy(left.from, left.to, temp);
                left.from = temp;

                for (;;)
                {
                    if (*right.from < *left.from)
                    {
                        *dest++ = *right.from;
                        if (++right.from == right.to)
                        {
                            copy(left.from, left.to, dest);
                            break;
                        }
                    }
                    else
                    {
                        *dest++ = *left.from;
                        if (++left.from == left.to) break;
                    }
                }
            }
            else if (ssl_to >= to || n == SSL_SZ)
            {
                // Merge right
                dest = right.to;
                right.to = copy(right.from, right.to, temp);
                right.from = temp;

                --left.to;
                --right.to;

                for (;;)
                {
                    if (*right.to < *left.to)
                    {
                        *--dest = *left.to;
                        if (--left.to < left.from)
                        {
                            copy(right.from, right.to + 1, --dest - (right.to - right.from));
                            break;
                        }
                    }
                    else
                    {
                        *--dest = *right.to;
                        if (--right.to < right.from) break;
                    }
                }
            }
            else
            {
                break;
            }

            // Update SSL info
            ssl[n - 2].to = ssl[n - 1].to;
            ssl[n - 2].size = ssl[n - 2].to - ssl[n - 2].from;
            --n;
        }
    }

    // Deallocate temp
    delete[] temp;
}

void printArray(int* arr, int size)
{
    for (int i = 0; i < size; ++i)
    {
        cout << arr[i] << " ";
    }
    cout << endl;
}

int main()
{
    // Prepare test data
    const int sz = 10;
    int* a = new int[sz];

    srand(time(0));

    for (int i = 0; i < sz; ++i)
    {
        a[i] = rand();
    }

    // Print array before sorting
    cout << "Before : ";
    printArray(a, sz);

    // Sort
    MSort(a, &a[sz]);

    // Print after sorting
    cout << "After : ";
    printArray(a, sz);

    // Deallocate array
    delete[] a;

    return 0;
 }

Code walkthrough:

• Function signature: the method takes two integer pointers. The first is pointing to the beginning of an array, where the other points to one element past the end of the array. The two pointers will serve as iterators over the array.
• The function begins by checking to see if there is more than one element in the array as arrays of one element are always sorted.
• Next, the function defines a structure that will hold SSLs found in the array. Fields inside the structure are: from which is the start of an SSL, to is one element past the end of the SSL. Finally, the size of the SSL.
• Next, is a definition of SSL size of hundred elements. It is more than enough as we execute merge after each new SSL addition, and we don’t wait till we gather all SSLs.
• Next, is a definition for the SSL array.
• Next, is a definition of two objects of SSL structure, they are used for merging, left is the left SSL to be merged where right is the right SSL.
• Next, is a definition of an integer to hold the number of SSLs currently in the SSL array.
• Next, is a definition of the size of the array we are sorting.
• Next, is a definition of the temporary storage used in merging routine.
• Next, is a definition of three integer pointers (iterators) the sslfrom and sslto are used in the gathering routine while the last one dest will be the position where merging will start.
• Next, is the beginning of the loop over the array, it will execute only once.
• Next, is the set of instructions to find SSLs. It compares the second element with the previous one and if it is greater then it will go ahead and find an ascending SSL. If it is less, then it goes ahead to find a descending SSL. If it is equal then advance and then compare again and not decide where we are going up or down until we find a greater or less element.
• Next, is the addition of the SSL we found to the SSL array.
• Next, is the merging routine. It runs only if we have more than one SSL and it merges only when the size of the right SSL is equal to or greater than the left SSL. This is to ensure that we merge SSLs that are similar or closer in size, as measurements show that merging equally sized sublists is more efficient. If they are not equal, it checks to see if we reached the end of the SSL gathering by examining the ssl_to variable, if so then it merges them as there are no more SSL will be added.
• Finally, the deallocation of temporary storage.

Environment used:

Visual Studio 2019 with C++ 17 was used in development and testing.

Stability:

• M Sort is a stable sorting algorithm.

Time Complexity:

• Best case: O (n)
• Average case: O (n log n)
• Worst case: O (n log n)

Space Complexity:

• O (n/2)

Notes:

1. A collection is any container of objects of a similar type like arrays, lists, or linked lists.
2. To be precise, an SSL could consist of one element as sometimes one element is left at the end of the collection, it is considered an SSL and it will get merged along with other SSLs.
3. n/2 should be calculated as ceiling(n/2) so if n = 15, then the maximum number of SSLs is 8.
4. We mean by completely random data, a collection with no SSLs with lengths of more than two, basically the worst case.