Magic Hexagon

Most of us are familiar with Magic Squares and its wonders. But little is known about Magic Hexagons. This post is attributed for describing "Magic Hexagons".

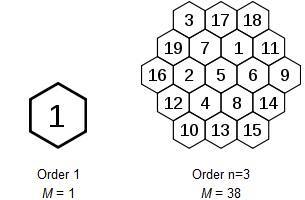
A magic hexagon of order n is an arrangement of numbers in a centered hexagonal pattern with n cells on each edge, in such a way that the numbers in each row, in all three directions, sum to the same magic constant. A normal magic hexagon contains the consecutive integers from 1 to 3n^2 − 3n + 1. It turns out that normal magic hexagons exist only for n = 1 (which is trivial) and n = 3. Moreover, the solution of order 3 is essentially unique. These hexagons are shown for your reference. The first magic hexagon has Magic sum 1 and second has Magic Sum 38.

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

This is interesting. Do you know why no other magic hexagon of higher orders exist?

With $n=2$ , why can't we have

$\begin{array} { l l l l } & 1 & & 2 \\ 5 & & 4 & & 3 \\ & 6 & & 7 \\ \end{array}$

The entries in each row sum to 12. Is there something that I'm missing?

Calvin Lin Staff - 7 years, 3 months ago

I believe what you wrote down isn't exactly correct. Although a few of the rows sum to 12, not all of them do. I'll go through a few of the rows.

$1 + 2 \neq 12$

$5 + 6 \neq 12$

$6 + 7 \neq 12$

and so on.

Milly Choochoo - 7 years, 3 months ago

Ah, even 'partial' rows count. That makes sense now. Thanks!

Calvin Lin Staff - 7 years, 3 months ago

Higher order magic hexagons do exist, but cannot be 'normal'.

Jonathan Wong - 7 years, 3 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$