Minimum Distance Between 2 Curves

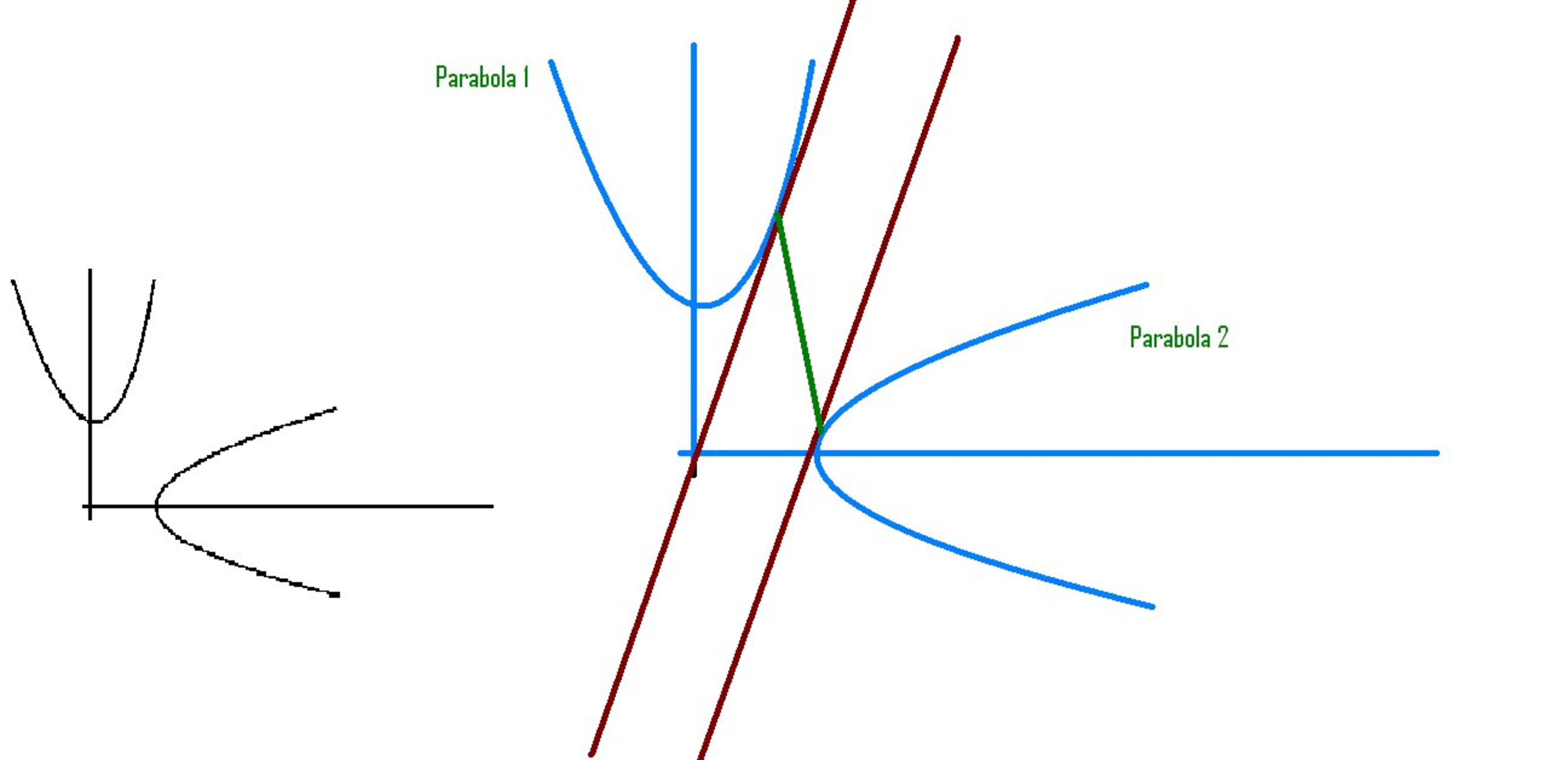
I was trying ( unsuccessfully ) to find the minimum distance between two parabolas and thought that I could do that by finding the minimum distance between two parallel tangents to the two parabolas. However there comes a case when ( as shown in figure ) the tangents are indeed parallel and the distance between them is also minimum but ( as shown by the green line ) the actual distance between the point of contacts is not the distance between the parallel lines but much more ... How do I do such problems ??

#Geometry #HelpMe! #MathProblem #Math

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Minimum distance will be along common normal. Use little calculus & co-ordinate geometry to get it.

Piyushkumar Palan - 7 years, 6 months ago

I don't think calculus will be needed....work using the parabola y^2=4ax....and use the parametric form of the equation i.e. (at^2,2at)...then write equation for both the normals and equate them....works beautifully!!!

Tanya Gupta - 7 years, 3 months ago

How can we equate them there would be two variable t1 and t2

Devkant Chouhan - 4 years, 7 months ago

Ooh! My favorite! You have to set up a distance formula, with each equation as a point! It's awesome! From there, you simplify, and use basic algebra to minimize! Great post!

Finn Hulse - 7 years, 3 months ago

so its like distance between (x,f(x)) and (y,g(y))

Sai Kalyaan Palla!!! - 3 years, 2 months ago

can be solved by making the equation in a variable involving parametric equations for the two curves .. try to get it in one single parameter and then differentiate to get the critical point.. !!

Ramesh Goenka - 7 years, 6 months ago

cool

jafar badour - 6 years, 3 months ago

You can find the symmetry line.......as an example y=x is the line of symmetry between y^2=4x and x^2=4y double the dist from one parabola to y=x and you get the distance

Saswata Dasgupta - 6 years, 1 month ago

lagrange methode in calculus maybe help

Abdul Siregar - 7 years, 6 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$