Mood

Find the exact value of the following expression:

\[1 \times \frac{1}{4} + \left(1 + \frac{1}{4} \right) \times \frac{1}{9} + \left(1 + \frac{1}{4} + \frac{1}{9} \right) \times \frac{1}{16} + \dots\]

I sought ways of manipulating numbers, coming up with the following a few years back:

Given a list of numbers, repeat this procedure for all terms and return the sum. For all terms, sum the previous terms and multiply that with the term itself.

An example: [3, 3, 4] would result to 3 x 3 + (3 + 3) x 4 = 33. [1, 2, 3, 4] would be 1 x 2 + 3 x 3 + 6 x 4 = 35. Lists with fewer than two terms are considered to result in 0. (This is not particularly interesting)

One property of this that quickly arose is that the order of the terms does not matter. e.g. [3, 3, 4] is equivalent to [4, 3, 3].

There are some quirky operations related to partitioning an element, modifying the list while keeping the sum the same, e.g. [3, 3, 4] + 2x2 + 1x2 - 3x1 + 2x2 → [3, 3, 2, 2] + 1x2 - 3x1 + 2x2→ [3, 1, 2, 2, 2] - 3x1 + 2x2 → [4, 2, 2, 2] + 2x2 → [2, 2, 2, 2, 2]

Below are a couple of problems that would hopefully prove interesting. Solutions follow. Level of complexity are relative to each other only.

Level 1

1. What happens to the result when I multiply all the terms in the list by n?

2. Implement in Python (sorry not sorry) the function Lolly, which takes in a list 'lst' and calculates its value as done above, given the following template.

*This is not the best implementation, as we shall see, but makes more sense immediately given the above definition.

    def Lolly(lst):
        """
        >>> Lolly([2, 1, 6])
        20
        """
        if __________:
            return __________
        return Lolly(__________) + __________

Level 2

It was not long before I experimented with infinite sequences. Find the result of the procedure applied to the infinite geometric progression with 1 as the first element and 0.5 as the ratio, i.e. [1, 0.5, 0.25, ...].

• Optional: Generalise this result with a as the first element and 1/r as the ratio.

Level 3

The generalised result from above is only valid for |1/r| < 1 that allows convergence. Find the result of the procedure applied to the finite geometric progression with 1 as the first element and 10 as the ratio, up until the nth term = 10^(n - 1).

• Optional: Generalise this result with a as the first element, 1/r as the ratio, up to n terms.

solutions

Everything revolves around the definitions made.

Level 1

1. The result is scaled by n squared. This is evident when you expand the expression algebraically, each term being a product of two elements - multiplying each individual element by n is equivalent to multiplying n squared to the entire expression. We will revisit this with another explanation from a slightly different point of view.

2. This is quite straightforward.

   def Lolly(lst):
       if len(lst) < 2:
           return 0
       return Lolly(lst[1:]) + lst[0] * sum(lst[1:])
   

Level 2

There is no trick other than to simply attempt this algebraically (yet). $\begin{aligned} &1 \times \frac{1}{2} + \left(1 + \frac{1}{2} \right) \times \frac{1}{4} + \left(1 + \frac{1}{2} + \frac{1}{4} \right) \times \frac{1}{8} + \dots\\ = &1 \times \left( \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \dots \right) + \frac{1}{2} \times \left( \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \dots \right) + \frac{1}{4} \times \left( \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \dots \right) + \dots\\ = &\left( \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \dots \right) \times \left(1 + \frac{1}{4} + \frac{1}{16} + \dots \right)\\ = &\frac{4}{3} \end{aligned}$

• Optional part, essentially identical

$\begin{aligned} &a \times \frac{a}{r} + \left(a + \frac{a}{r} \right) \times \frac{a}{r^2} + \left(a + \frac{a}{r} + \frac{a}{r^2} \right) \times \frac{a}{r^3} + \dots\\ = &a \times \left( \frac{a}{r} + \frac{a}{r^2} + \frac{a}{r^3} + \dots \right) + \frac{a}{r} \times \left( \frac{a}{r^2} + \frac{a}{r^3} + \frac{a}{r^4} + \dots \right) + \frac{a}{r^2} \times \left( \frac{a}{r^3} + \frac{a}{r^4} + \frac{a}{r^5} + \dots \right) + \dots\\ = &\left( \frac{a}{r} + \frac{a}{r^2} + \frac{a}{r^3} + \dots \right) \times \left(a + \frac{a}{r^2} + \frac{a}{r^4} + \dots \right)\\ = &\frac{a^2r^2}{ \left(r - 1 \right)^2 \left(r + 1 \right)} \end{aligned}$

Level 3

$\begin{aligned} &1 \times 10 + \left(1 + 10 \right) \times 100 + \left(1 + 10 + 100 \right) \times 1000 + \dots + \left(1 + 10 + 100 + \dots + 10^{n - 2} \right) \times 10^{n - 1}\\ = &1 \times \left(10 + 100 + 1000 + \dots + 10^{n - 1} \right) + 10 \times \left(100 + 1000 + 10000 + \dots + 10^{n - 1} \right) + \dots + 10^{n - 3} \times \left(10^{n - 2} + 10^{n - 1} \right) + 10^{2n - 3}\\ = &\frac{10^n - 10}{9} + 10 \times \frac{10^n - 100}{9} + \dots + 10^{n - 3} \times \frac{10^n - 10^{n - 2}}{9} + 10^{n - 2} \times \frac{10^n - 10^{n - 1}}{9}\\ = &\frac{10^n}{9} \times \left(1 + 10 + 100 + \dots + 10^{n - 2} \right ) - \frac{10}{9} \times \left(1 + 10^2+ 100^2 + \dots + 10^{2n - 4} \right)\\ = &\frac{10^n}{9} \times \frac{10^{n - 1} - 1}{9} - \frac{10}{9} \times \frac{100^{n - 1} - 1}{99}\\ = &\frac{ \left(10^n - 10 \right) \left(10^n - 1 \right)}{891} \end{aligned}$

• optional part

$\begin{aligned} &a \times \frac{a}{r} + \left(a + \frac{a}{r} \right) \times \frac{a}{r^2} + \left(a + \frac{a}{r} + \frac{a}{r^2} \right) \times \frac{a}{r^3} + \dots + \left(a + \frac{a}{r} + \frac{a}{r^2} + \dots + \frac{a}{r^{n - 2}} \right) \times \frac{a}{r^{n - 1}}\\ = &a \times \left( \frac{a}{r} + \frac{a}{r^2} + \frac{a}{r^3} + \dots + \frac{a}{r^{n - 1}} \right) + \frac{a}{r} \times \left( \frac{a}{r^2} + \frac{a}{r^3} + \frac{a}{r^4} + \dots + \frac{a}{r^{n - 1}} \right) + \dots + \frac{a}{r^{n - 3}} \times \left( \frac{a}{r^{n - 2}} + \frac{a}{r^{n - 1}} \right) + \frac{a^2}{r^{2n - 3}}\\ = &\frac{a^2r^{1 - n} - a^2}{1 - r} + \frac{a^2r^{- n} - a^2r^{-2}}{1 - r} + \dots + \frac{a^2r^{4 - 2n} - a^2r^{6 - 2n}}{1 - r} + \frac{a^2r^{3 - 2n} - a^2r^{4 - 2n}}{1 - r}\\ = &\frac{a^2r^{1 - n}}{1 - r} \left(1 + r^{-1} + r^{-2} + \dots + r^{2 - n} \right) - \frac{a^2}{1 - r} \left(1 + r^{-2} + r^{-4} + \dots + r^{4 - 2n} \right)\\ = &\frac{a^2r^{1 - n}}{1 - r} \times \frac{r^{2 - n} - r}{1 - r} - \frac{a^2}{1 - r} \times \frac{r^{4 - 2n} - r^2}{1 - r^2}\\ = &\frac{a^2 r^{2 - 2n} \left(r^n - 1 \right) \left(r^n - r \right)}{ \left(r - 1 \right)^2 \left(r + 1 \right)} \end{aligned}$

Probably faster would be to reuse the result from Level 2.

Before I continue, allow me to introduce the actual name of this construct - this is known as the 2nd elementary symmetric polynomial, as I had recently discovered (to my disappointment that someone beat me to it).

We continue with one more problem.

Level 4

This part is crucial. We revisit the definition. With all things considered, find a more convenient way to find the result from the procedure given some list. Implement newLolly with the same behaviour as Lolly with the following template.

def newLolly(lst):
    return __________ #lol good luck

solution

Eventually Python refused to comply when the recursion limit was reached (frequently). I was forced to come up with some way to speed up the process and prevent Python from stopping altogether.

We can represent a product by a rectangle where the sides are the multiplicands. With the expressions from this procedure, one can construct a staircase out of these rectangles.

  3 3 4       each X represents a rectangle
3|
3|X           3x3
4|X X         3x4 + 3x4
[3, 3, 4] = 33

  1 2 1 2
1|
2|X           1x2
1|X X         1x1 + 2x1
2|X X X       2x1 + 2x2 + 2x1
[1, 2, 1, 2] = 13

But wait! I have just constructed a square with the diagonal and the other half taken out, the side length of the square being the sum of all elements in the list.

So it turns out that the result is equivalent to the square of the sum of all the elements in the list subtracted by the square of each element all divided by 2.

def newLolly(lst):
    return (sum(lst) ** 2 - sum([i ** 2 for i in lst])) / 2

In the problems of Levels 2 and 3, the first step in both solutions is merely grouping rectangles in a different way, horizontally to vertically.

On a side note, changing the order of elements in a list is like moving rectangles and doesn't change the area.

All the above is likely the same as this.

With a similar setup, this can be extended to higher order elementary symmetric polynomials using cubes (3rd) / hypercubes.

Let's revisit the previous problems with all of this in mind.

Level 1

1. Think of the square. Multiplying all lengths by n is equivalent to scaling all areas by n squared. It follows naturally that the result is scaled by n squared.

Level 2

We now attempt this problem with the new method.

$\begin{aligned} &\frac{1}{2} \left[ \left(1 + \frac{1}{2} + \frac{1}{4} + \dots \right)^2 - \left(1 + \frac{1}{2^2} + \frac{1}{4^2} + \dots \right) \right]\\ = &\frac{1}{2} \left[4 - \frac{4}{3} \right]\\ = &\frac{4}{3} \end{aligned}$

• Optional part

$\begin{aligned} &\frac{1}{2} \left[ \left(a + \frac{a}{r} + \frac{a}{r^2} + \dots \right)^2 - \left(a^2 + \frac{a^2}{r^2} + \frac{a^2}{r^4} + \dots \right) \right]\\ = &\frac{1}{2} \left[ \frac{a^2r^2}{ \left(r - 1 \right)^2} - \frac{a^2r^2}{r^2 - 1} \right]\\ = &\frac{a^2r^2}{ \left(r - 1 \right)^2 \left(r + 1 \right)} \end{aligned}$

Level 3

$\begin{aligned} &\frac{1}{2} \left[ \left(1 + 10 + 100 + \dots + 10^{n - 1} \right)^2 - \left(1 + 10^2 + 100^2 + \dots + 10^{2n - 2} \right) \right]\\ = &\frac{1}{2} \left[ \frac{ \left(10^n - 1 \right)^2}{81} - \frac{100^{n} - 1}{99} \right]\\ = &\frac{ \left(10^n - 10 \right) \left(10^n - 1 \right)}{891} \end{aligned}$

Armed with the new weapon, we return to the very first problem.

Level 5

Find the exact value of the following expression:

$1 \times \frac{1}{4} + \left(1 + \frac{1}{4} \right) \times \frac{1}{9} + \left(1 + \frac{1}{4} + \frac{1}{9} \right) \times \frac{1}{16} + \dots$

solution

To manipulate this algebraically to find the answer is not easy, but notice that this is just [1, 1/4, 1/9, ...] expanded. The previous method is applicable (paired with assumed knowledge of z(2) and z(4)).

$\begin{aligned} &\frac{1}{2} \left[ \left(1 + \frac{1}{2^2} + \frac{1}{3^2} + \dots \right)^2 - \left(1 + \frac{1}{2^4} + \frac{1}{3^4} + \dots \right) \right]\\ = &\frac{1}{2} \left[ \frac{ \pi^4}{36} - \frac{ \pi^4}{90} \right]\\ = &\frac{ \pi^4}{120} \end{aligned}$

What's next?

Play with what we have! Plug in diverging sequences, investigate other kinds of sequences, all the good stuff.

extras

Find out what's wrong with this OEIS entry. (photo taken at the time of writing, corrections are being made and published soon)

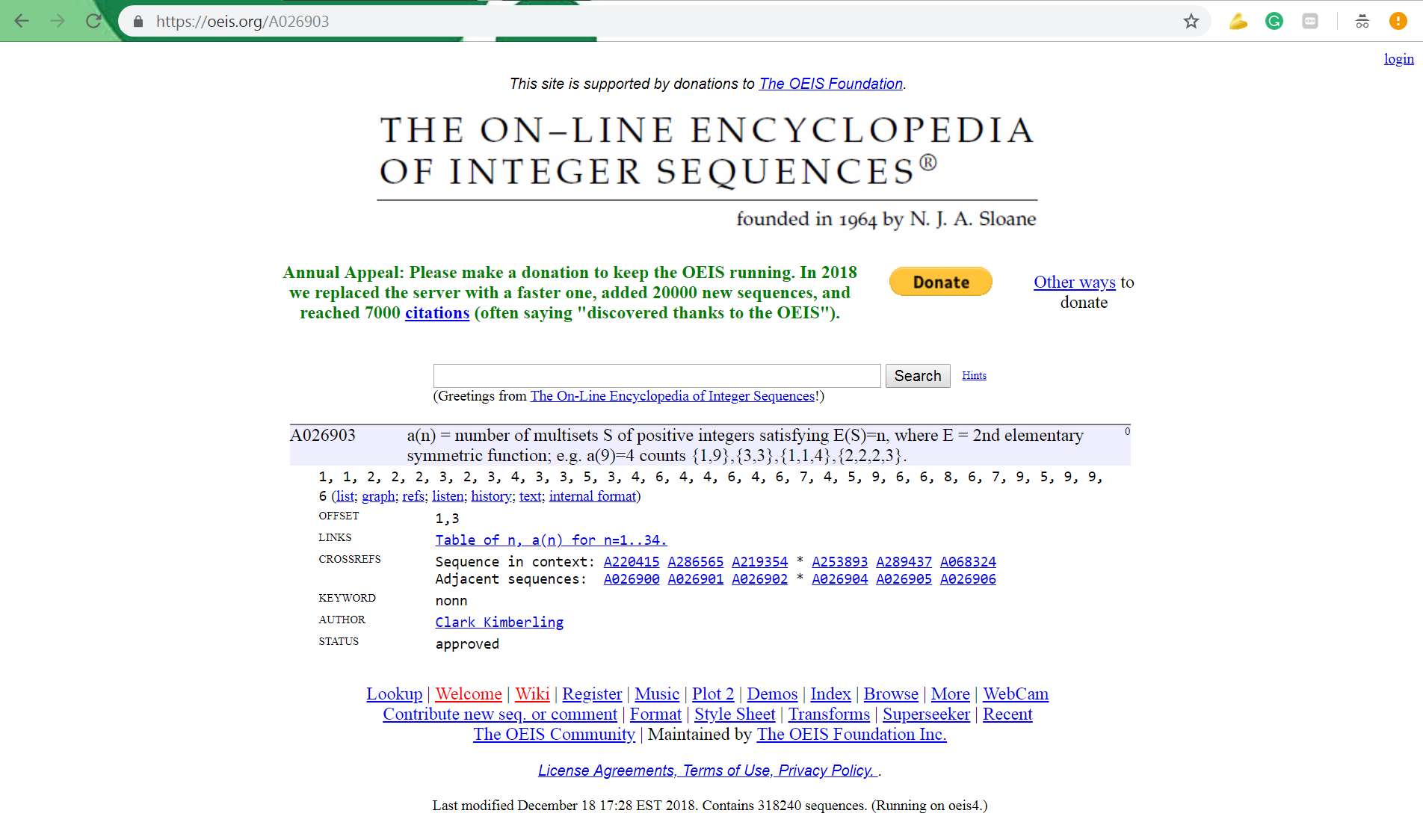
Implement invLolly(n) which returns the list of 'multisets' as described in A260903; len(invLolly(n)) should return a(n). (This is my rather basic and easy-to-understand implementation, probably not the fastest but better than nothing; a PARI program written by Andrew Howroyd will be made available on the OEIS page.)

def invLolly(n):
    """
    >>> invLolly(24)
    [[1, 1, 1, 2, 3], [1, 1, 1, 7], [1, 4, 4], [1, 24], [2, 2, 2, 2], [2, 2, 5], [2, 12], [3, 8], [4, 6]]
    >>> len(invLolly(900))
    3214
    """
    current = [1]
    reps = []
    while __________:
        while __________:
            current.append(__________)
        if __________:
            reps.append(__________)
        __________ = __________
    return reps