Most common number of prime factors

I wrote some Python code to check what the most common number of prime factors is for all numbers between $1$ and $1,000,000$ (it took a while!). For example, $10$ has two prime factors, $2$ and $5$ , and $220$ has four: $2$ , $2$ , $5$ , and $11$ . Here's what I got:

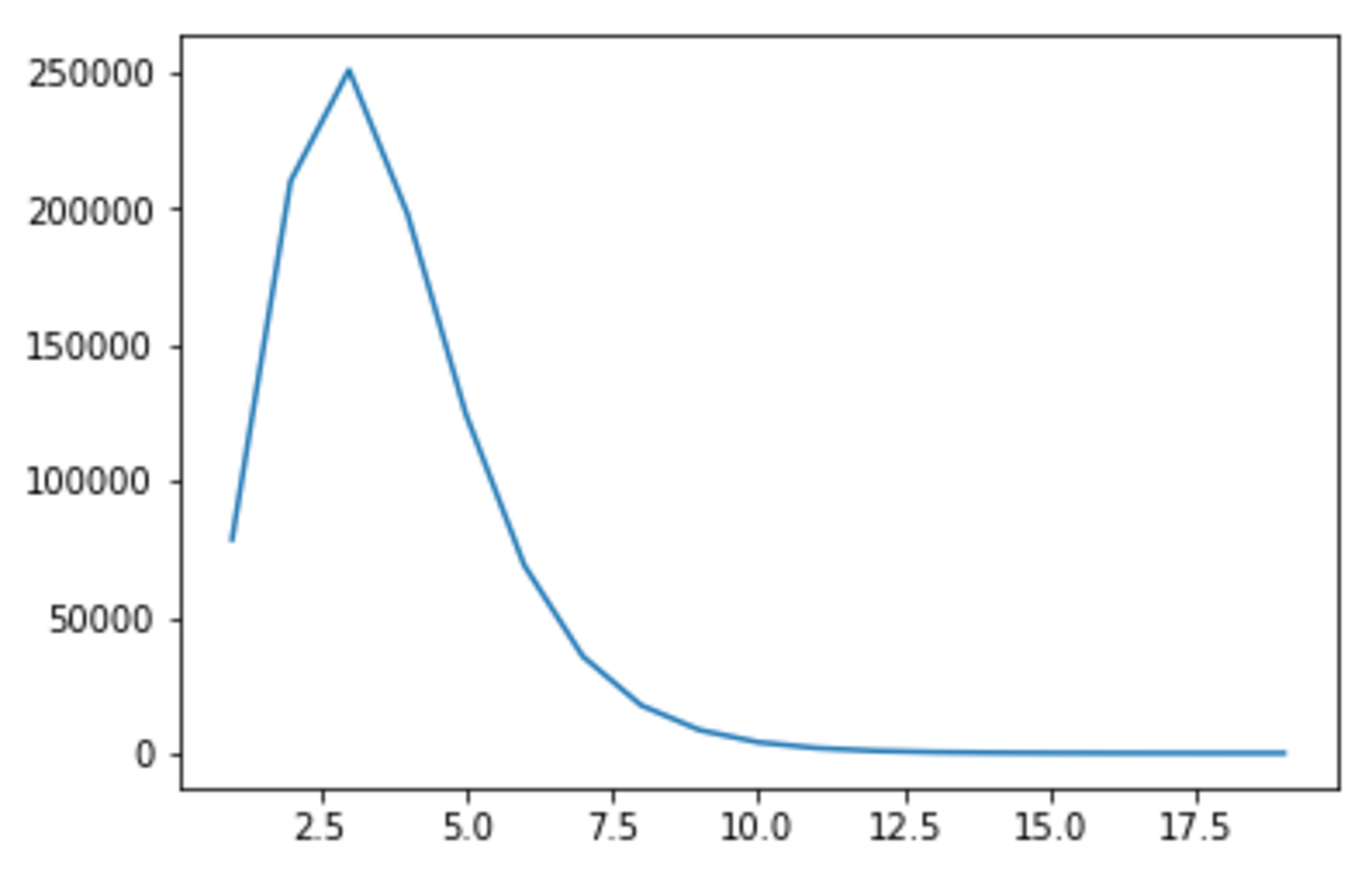
(Please forgive the odd x-axis scale. I forgot to set this before I ran the program.)

At first I checked numbers between $1$ and $10,000$ , and then $1$ and $100,000$ , and when I did this, it appeared that it was most common for a number to have $2$ prime factors. But as I increased the upper bound, $3$ prime factors became the most frequent.

I'm not sure if this would change once again with an even larger upper bound, because my laptop took about 20 minutes to do up to $1,000,000$ . Does anyone have anything to add?

#NumberTheory

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

You could ask @Zakir Husain, @David Stiff.

Yajat Shamji - 11 months, 2 weeks ago

@David Stiff - I have organised a discussion in which a code is share, we will execute it but by breaking into pieces (together) as it will take much longer time if executed by me alone. For more information click here, hope we will go beyond $10^9$ !

Zakir Husain - 11 months, 1 week ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$