Muhammad's strings

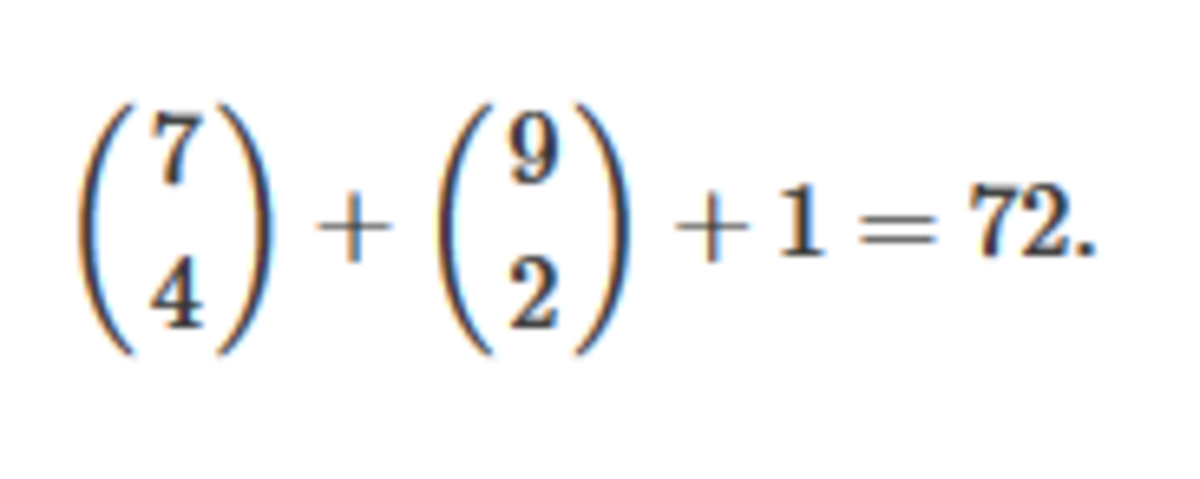
this concept in the picture was used to solve the problem, but I don't know about this concept and I couldn't search for it in Google . it apparently isn't matrix

#HelpMe! #MathProblem

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

its 7 choose 4 and 9 choose 2, counting...

Kee Wei Lee - 7 years, 11 months ago

OK thank you I just didn't know that way of writing choose

Abdo Saeed - 7 years, 11 months ago

after thinking in the problem for a while I couldn't realize why thy have calculated it this way I know the concept of choose but I couldn't relate it with what they have done if you don't know th problem and the answr here they are How many strings of ones and zeros of length 10 are there such that there are no consecutive zeros and an even number of ones? First, we observe that if there are 4 or fewer ones, then two zeroes must be next to each other.

If there are 6 ones, then the 4 zeroes can go in 7 possible positions, and there are (74) ways to do this. If there are 8 ones, then the remaining 2 zeros can go in 9 possible positions, giving (92) ways. If there are 10 ones, there are no zeros to be placed. Thus, the answer is

I don't understand this part "then the 4 zeroes can go in 7 possible positions, and there are (74) ways to do this" sorry for disturbing

Abdo Saeed - 7 years, 11 months ago

okay consider _ 11111_1 _. Here there are six 1s' and seven _ spaces. Since we cannot place two consecutive 0s' together we have to place them in the _ spaces. So we have 7 places to put 4 zeroes, (7 4)

Kee Wei Lee - 7 years, 11 months ago

@Abdo It's best for you to make such comments in the solution discussion itself.

Note that the link is customized to you, and no one else will be able to view it. You need to use the "Share this problem" link instead. I've removed the link you provided.

Calvin Lin Staff - 7 years, 11 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$