Multivariable limits

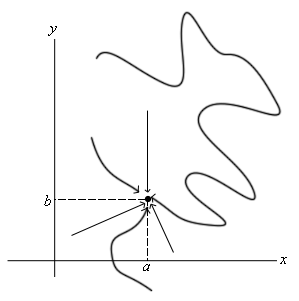
Recently, I've just learn about multivariate limits in my Advanced Calculus class. The concept is such that there are infinite possible approaches in solving limit problems (see picture). Why would it not be sufficient to just consider the direct displacement of our approach? If there is a direct displacement from all directions, it would form an area such that all paths taken falls within the area. Hence, if the limit of the direct displacement exists, we can safely conclude that the limits of all paths exists.

If that is the case, we can simply let $y=mx, m\in\mathbb{R}$ and solve the limits. I will show my approach in multivariate problems in the following forms. Consider $4$ cases, $\lim_{(x, y)\rightarrow(0, 0)}f(x, y)$, $\lim_{(x, y)\rightarrow(a, 0)}f(x, y)$, $\lim_{(x, y)\rightarrow(0, b)}f(x, y)$ and $\lim_{(x, y)\rightarrow(a, b)}f(x, y)$ where $a, b\neq0$. In all cases, let $y=mx$.

Case $1$: $\lim_{(x, y)\rightarrow(0, 0)}f(x, y)$ $\because x, y\rightarrow0, \therefore m=\mathbb{R}$ $\therefore\lim_{(x, y)\rightarrow(0, 0)}f(x, y)=\lim_{(x, mx)\rightarrow(0, 0)}f(x, mx)\Rightarrow \lim_{(x, y)\rightarrow(0, 0)}f(x, y)=\lim_{x\rightarrow0}f(x, mx)$

If the multivariate limit exists, then $\lim_{(x, y)\rightarrow(0, 0)}f(x, y)=\lim_{x\rightarrow0)}f(x, mx)=L, L\in\mathbb{R}$, Else, $\lim_{x\rightarrow0}f(x, mx)=g(m)$ and the limit does not exist.

Case $2$: $\lim_{(x, y)\rightarrow(a, 0)}f(x, y)$ $\because x\rightarrow a, y\rightarrow0, \therefore m\rightarrow0$ $\therefore\lim_{(x, y)\rightarrow(a, 0)}f(x, y)=\lim_{(x, m)\rightarrow(0, 0)}f(x, mx)\Rightarrow\text{Case 1}$ And repeat the process of case $1$ to obtain the answer.

Case $3$: $\lim_{(x, y)\rightarrow(0, b)}f(x, y)$ $\because x\rightarrow0, y\rightarrow b, \therefore m\rightarrow\frac{b}{0}\rightarrow\infty$ $\therefore\lim_{(x, y)\rightarrow(0, b)}f(x, y)=\lim_{(x, m)\rightarrow(0, \infty)}f(x, mx)$ Then, let $m=\frac{1}{t}$. Hence, $t\rightarrow0$ as $m\rightarrow\infty$. This gives us $\lim_{(x, m)\rightarrow(0, \infty)}f(x, mx)=\lim_{(x, \frac{1}{t})\rightarrow(0, 0)}f(x, \frac{x}{t})\Rightarrow\text{Case 1}$

Case $4$: $\lim_{(x, y)\rightarrow(a, b)}f(x, y)$ $\because x\rightarrow a, y\rightarrow b, \therefore m=\frac{b}{a}$ $\therefore\lim_{(x, y)\rightarrow(a, b)}f(x, y)=\lim_{x\rightarrow a}f(x, \frac{b}{a}x)$

Note: Reducing the multivariate limits to a single variable limit allows the use of L'hopital's Rule. I have tested on many (but not all) problems to prove that the method works.

Any faults about the idea?