My Conjecture (not much important , not much trivial)

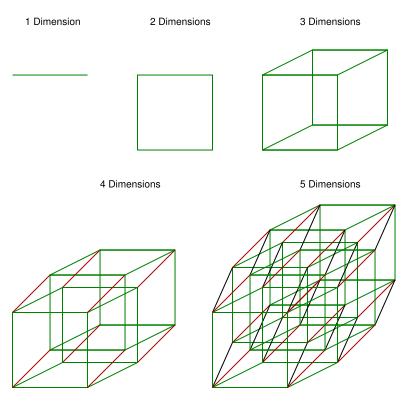
We know that we all live in the 3 dimensional world. In our real life we refer all things as "3D" objects. Since we are living in 3D world , it is quite easy for us to imagine the things which are one or two dimensional.But its very difficult for us to imagine things of 4,5,6... dimensions. So my conjecture states that :

" If a person thrives in a "n" dimensional world , it is easy for him to imagine the objects of the previous "(n-1)"and nth dimensions but its very difficult for him/her to imagine objects of dimensions greater or equal to "(n+1)".

Please post your opinions/discussions below.

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Whenever someone talks about an n-dimensional space I get very confused and dont understand even a single thing

Aditya Chauhan - 6 years ago

Yeah , it even happens with me!

Nihar Mahajan - 6 years ago

In the physical sense, "living in an n-dimensional world" just means that an entity is able to physically interact with all the dimensions of said world. This indirectly means that the entity has sense organs/machines which enable it to do so. Since all dimensions less than n are degenerate cases of the entity's world, it can interact with them with ease. But the same is not true for higher dimensions. The entity may or may not have sense organs/machines which can perceive and/or comprehend these higher dimensions. The entity may not even realize that it has the ability to understand higher dimensions.

Raghav Vaidyanathan - 6 years ago

How would you go about proving the conjecture?

Beakal Tiliksew - 6 years ago

I don''t know , unless we get a person not living in our world. :P

Nihar Mahajan - 6 years ago

Due to evolution, an n-dimension being would evolve a brain which would be able to understand an n-dimension object since it is required for survival, which would in turn make it easy for it to visualise dimensions lower than n because higher dimension objects are made of lower dimension objects, ie, a cube can be seen to be made of an infinite stack of squares.

Julian Poon - 6 years ago

@Julian Poon – Thats right. Since you are saying that "higher dimension objects are made of lower dimension objects" , then a (n+1) or even higher dimension object is made up of n dimension objects , then why is it so difficult for that being to imagine it?

Nihar Mahajan - 6 years ago

@Nihar Mahajan – because our brains are not accustomed to visualising objects made out of an infinite number of objects in the highest dimension we can imagine. Nature need not spend to much "resources" to evolve a brain that can imagine a higher dimension object since it is redundant in understanding the environment... just some of my thoughts...

Additionally, the physical environment also makes it impossible to see higher-than-n dimensions in a n dimension environment. This is so because seeing, say, in 4 dimensions in our 3 dimension world means seeing the insides of any 3 dimension object. I should be able to see your heart beating, if I can see 4 dimensions. However, hardly any (if any) photons of the visible length reflects off your heart and into my eyes. This makes it redundant for nature to enable the brain to visualise higher dimensions since it is not relevant.

Julian Poon - 6 years ago

each point in nth dimension gives rise to n lines . can you please tell me why is it so

harish ghunawat - 6 years ago

I mean, is there a good way to think about 4-dimensional?

Ashwin Padaki - 6 years ago

Superstring theory would help you proving your conjecture :-)

Swapnil Das - 6 years ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$