My Elasticity Doubt

Hey guys. I had a question on elasticity which looked something like this.

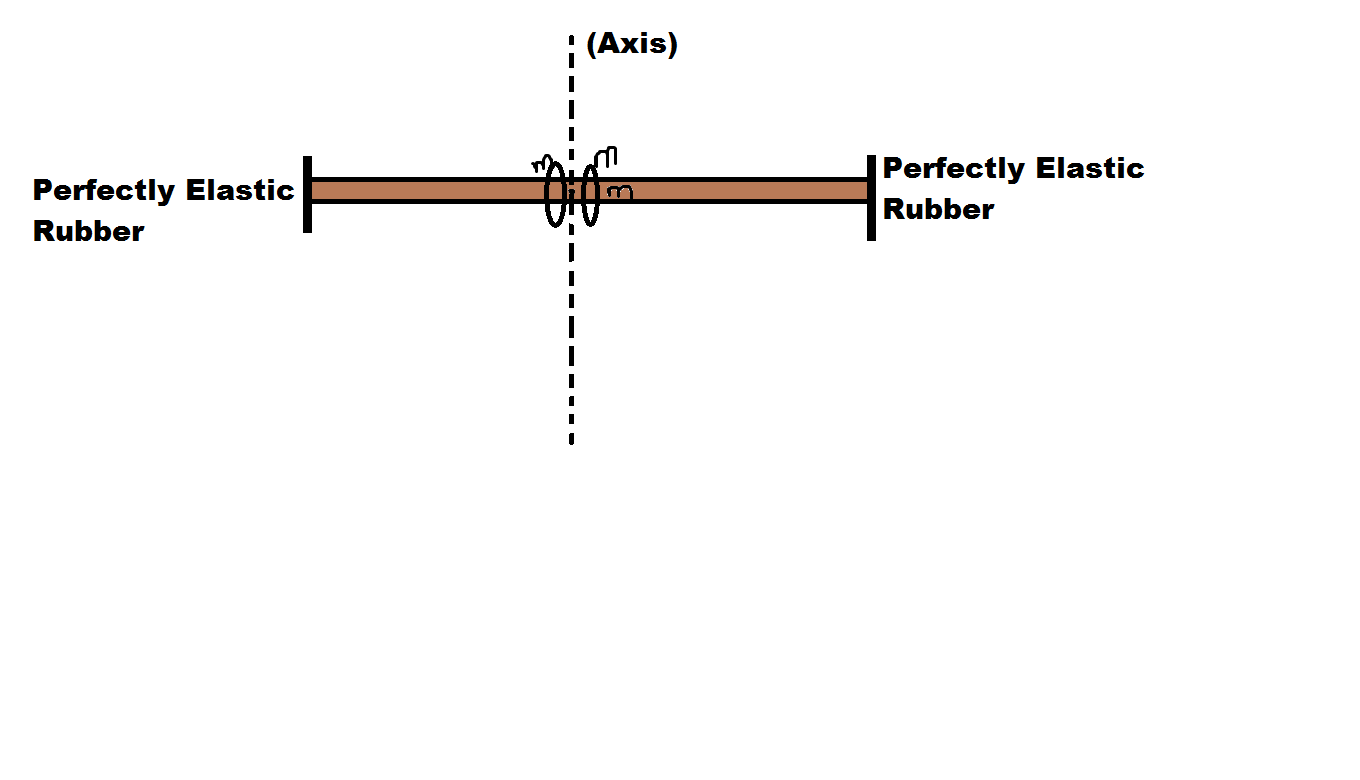
We have small beads of mass say \(m\) and Mass of rod say \(M\). Now we need to find the extension in the rod after the beads collide with the the perfectly elastic rubber. Given that it rotates with angular speed \(\omega\) and

$\text{Young's Modulus} = Y$ and $\text{Area}=A$. [And if you need more variable you can take it. I think the given variables are enough]

No friction is there between the beads.

Now see my solution.

Plan

We have a rotating rod. So we will find out the extension for rotation (Say $x_{1}$) and for the collision say $x_{2}$.

So is it that we need to find out $x_{1}+x_{2}$.

Now we can find $x_{1}$ easily as follows.

Lets take a differential portion of the rod as $dx$.

Now the mass of the differential mass = $dm = \lambda dx$

As rod is uniform we have $\lambda = \dfrac{M}{L}$

$\implies dm= \dfrac{M}{L} dx$.

Now We Stress= $\dfrac{Force}{Area}$

$\implies Stress = \dfrac{dm \omega^2 x}{A}$

$\implies Stress = \dfrac{M \omega^2 dx}{AL}$

$\implies \dfrac{Stress}{Strain} = Y$

$\implies \dfrac{M \omega^2 x^2 dx}{YAL} = d(\Delta x)$

Integrating from $-L \rightarrow +L$ we get

$\implies \Delta x = \dfrac{2M \omega^2 L^2}{3AY} = x_{1}$

Now we have the $x_{2}$ part.

For $x_{2}$. Can we say that the force exerted by each mass on the rod is $m \omega^2 L$ and then

$F= 2 m \omega^2 l$

$\implies \Delta x_{2} = \dfrac{2m \omega^2 L^2}{YA}$

So We can take $x_{1}+x_{2} = \dfrac{2 M \omega^2 L^2 + 6m \omega^2 L^2}{3YA}$

But i am confused if i can take the sum or if the beads play any role in extension or not.

PLEASE HELP!