Mysterious Art of Handling Trigonometric Ratios

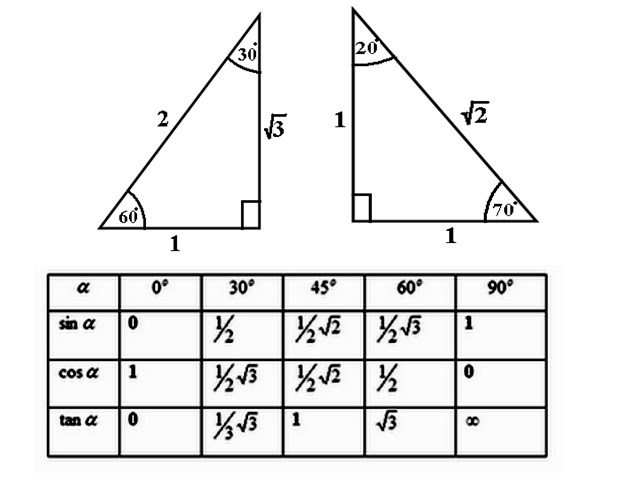
Weeks back, when I first had my trigonometric lesson, I was taught the simple basic identities of trigonometric ratios for special angles such as $30^0$ , $45^0$ and $60^0$ not forgetting right angles and zeroes too. Then it hit me, while I may had basic prior knowledge of trigonometry back then before the new lesson, I wondered how did trigonometric ratios such as $tan, cos and sin$ even came about in the first place? Is there a certain pattern or formula or any other that may allow me to retrieve the values of Trigo. ratios for any angles quickly without the use of calculator? Is it possible to mentally calculate trigonometric ratios for any angle as fast as multiplying numerical values such as $5\times 7$ ? Though I know it is pretty hard to answer it now or there may not even be an answer to these questions. However, I believe in time to come, the secret to mental calculation of trigo. ratios may be discovered. I hope the note isn't overly-ambitious on the impossible....

#Geometry

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Use the infinite expansion of both $\sin$ and $\cos$ if you don't have calculator. At least you would get approximate answer using only a few terms. For problems, usually the ratios can be found using sum and difference, double angle and half angle, etc.

Marc Vince Casimiro - 6 years, 5 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$