Need help here!
Given \( 2 \) circles with centres \( O \) and \( O^{'} \) in the Euclidean plane, one draws a couple of transverse common tangents to these circles, \( T_{1} \) and \( T_{2} \), and mark their intersection point as \( M \). Prove that \( M \) lies on \( OO^{'} \).
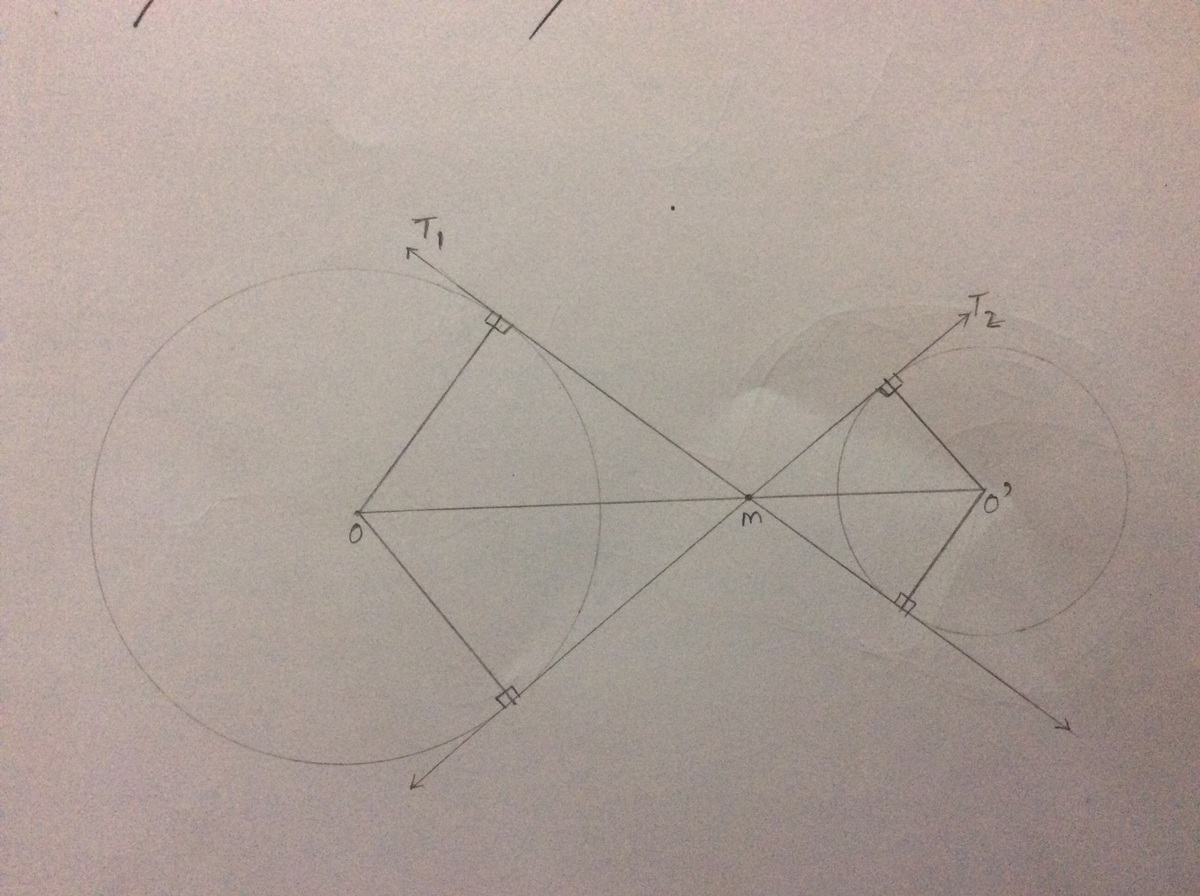 .
.
No vote yet
1 vote
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
@Xuming Liang @Nihar Mahajan @Daniel Liu
Log in to reply
This is clear by symmetry.
This is essentially homothety, consider the following proof:
Suppose the tangents intersect OO′ at M1,M2. Prove that O′M1OM1=O′M2OM2 and that this is sufficient to conclude that M1=M2=M.
Log in to reply
Thank You !
Log in to reply
You could also bash the problem and prove that M lies on the equation of OO'.
Log in to reply
Yeah, but I don't like it. I only like Euclid-style proofs, they are more beautiful.
Log in to reply
Yes u r right euclid style proofs r really awsome. but they require high level intuition. bashing doesn't require much intuition.