Newton Raphson method of root aproximation

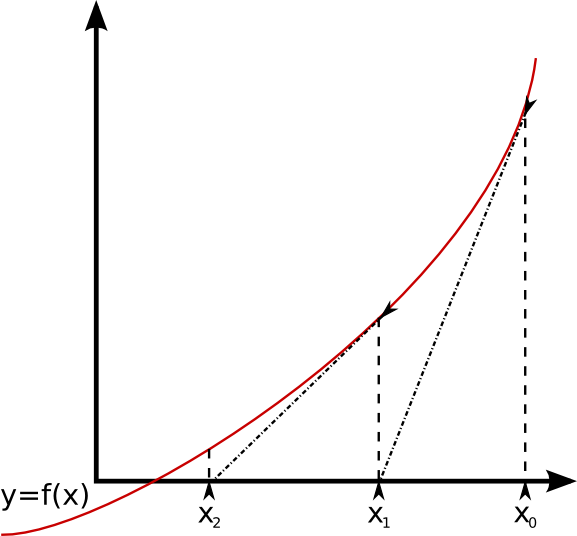
The Newton Raphson method finds successively better approximations to roots of the real valued function \( f(x) = 0 \).

Refer to the above image. We start off with the approximate root x0 x_0, find the value of f(x0) f(x_0) , take the tangent to the curve, which results in the approximate root x1x_1. We continue this process, find the value of f(x1) f(x_1) , take the tangent to the curve, which results in the approximate root x2x_2 . By continuing the process, we should reach the actual root x∗ x^* , to a great degree of accuracy.

Let's write this down in equation form. We start off with a first approximation, which is denoted by x0 x_0 . Then, we consider the point (x0,f(x0) (x_0, f(x_0) , which has a slope of f′(x0) f'(x_0) , hence the equation of the tangent is

y−f(x0)x−x0=f′(x0) \frac{ y - f(x_0) } { x - x_0 } = f' (x_0)

and the intersection with the x-axis occurs when y=0 y=0 , or that

x1=x0−f(x0)f′(x0). x_1 = x_0 - \frac{ f(x_0)} { f'(x_0)} .

We repeat this process with

xn+1=xn−f(xn)f′(xn), x_{n+1} = x_n - \frac{ f(x_n) } { f'(x_n) },

until a sufficiently accurate value is reached.

Find the value of 2 \sqrt{2} as the root of the equation f(x)=x2−2 f(x) = x^2 -2 , using the starting value of x0=2 x_0 = 2 . Note that all values of xnx_n will be rational numbers, hence we get a sequence of rationals which approximate the value of the irrational number 2 \sqrt{2} .

#Calculus #RootApproximation #NewtonRaphsonMethod

Note by Chung Gene Keun
7 years, 2 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

Ahh!? Finally, there is someone here make a note about this topic. Now, using the Newton-Raphson method, try to answer these problems:

  1. Simultaneous Linear Equations

  2. Simultaneous Non-Linear Equations

  3. Computational Physics (Mechanical System)

Good luck!! (^_^)

Tunk-Fey Ariawan - 7 years, 2 months ago

Ugh!!I wanted to make a note on this topic....but you beat me to it!!Nicely presented btw!!

Eddie The Head - 7 years, 2 months ago

Log in to reply

Thanks! I wanted to create problems on the Newton Raphson method, and highlight the cases when it failed, as those were interesting to me.

I found that explaining this method in the problem made it too long, so I separated it out into a note, and will link it from there. Problems should be posted soon :)

Chung Gene Keun - 7 years, 2 months ago

Here, f(x) = x^2 - 2 and f’(x) = 2x

Now, f(0)=-2

f(1)=-1

f(2)=0

f(3)=7

hence, the root lies between 1 and 2.

Let, x0 = 1

x1 = x0 – { f(x0) / f’(x0)}

 = 1 – {(-1) / 2}

 = 1.5

Similarly,

x2 = 1.4166

x3 = 1.4142

x4 = 1.4142

hence, √2 = 1.4142

Debika Sadhukhan - 7 years, 1 month ago

IS BISECTION METHOD AND REGULA-FALSI METHOD SAME OR DIFFERENT..???

Santhosh HD - 6 years, 9 months ago

Isnt it better to use it to approximate roots of higher degree equations than finding square roots?

Deepak Pant - 6 years, 6 months ago
×

Problem Loading...

Note Loading...

Set Loading...