Tough Gravitation problem

A uniform solid sphere has a Mass M and radius R. From it , a solid sphere of radius R/2 is removed and taken to infinity . Can anyone help to calculate the work done by external agent to achieve this ? 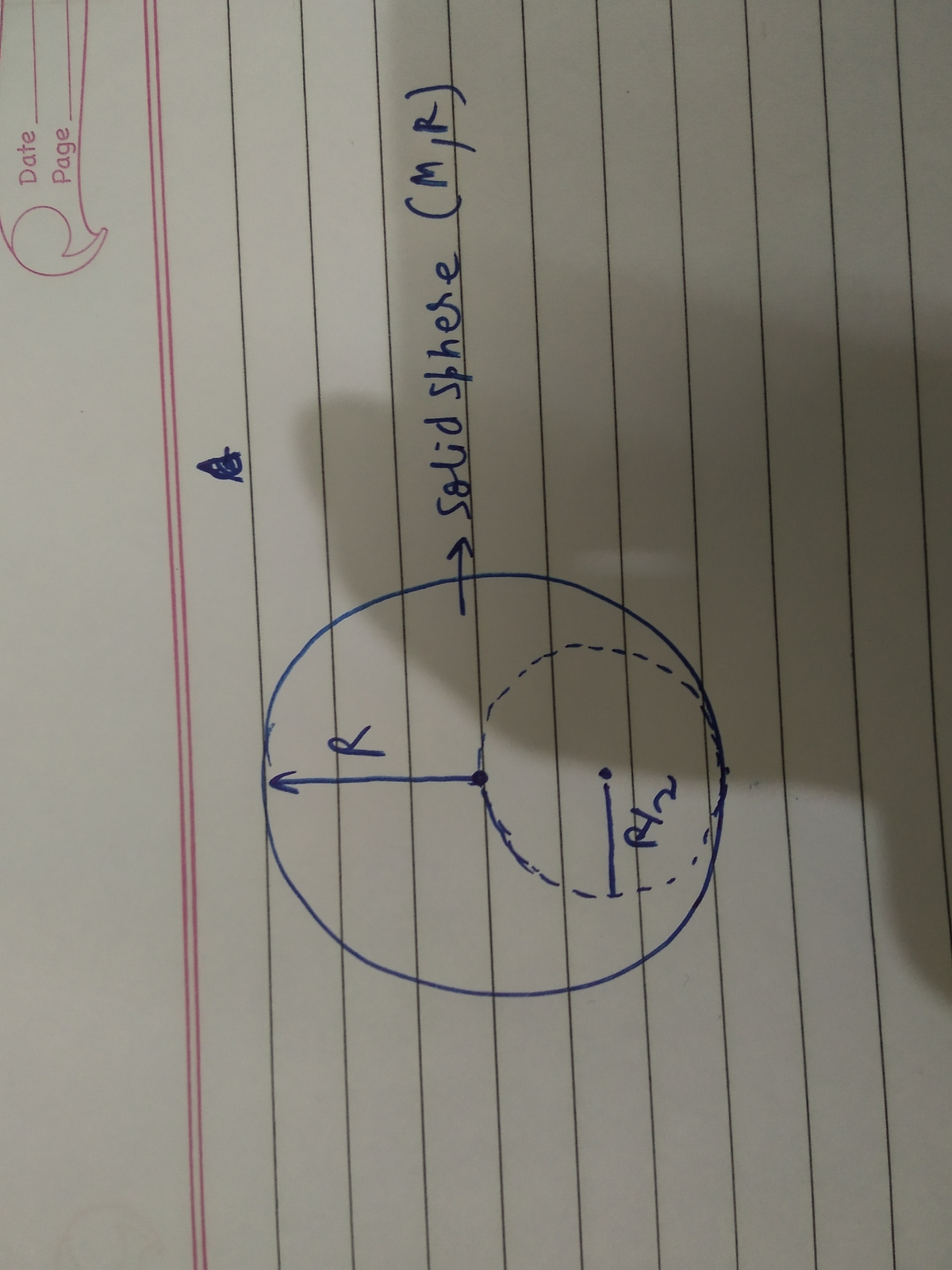( Can integration over three dimensions be avoidef here ?) ( I am not getting how to solve as the gravitatonal field will be not uniform inside the cavity sphere )

#Mechanics

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Integrating numerically, I get very nearly $\frac{G M^2}{8R}$ .

import math

N = 500   # simulation resolution

##########################################

# Constants

M = 2.7   # Full sphere mass
R = 1.3   # Full sphere radius
G = 11.1  # Grav constant

V = (4.0/3.0)*math.pi*(R**3.0)  # Full sphere volume

rho = M/V  # density

Rs = R/2.0  # small sphere radius

Vs = (4.0/3.0)*math.pi*(Rs**3.0)  # Small sphere volume
Ms = Vs * rho   # Small sphere mass

U_ref = G*(M**2.0)/(8.0*R)  # Reference value of work done - for comparison

##########################################

# Infinitesimals for integration

dr = R/N
dtheta = 2.0*math.pi/N
dphi = math.pi/N

##########################################

r = 0.0

U = 0.0

count = 0

while r <= R:    # Integrate over interior of large sphere

    theta = 0.0

    while theta <= 2.0*math.pi:

        phi = 0.0

        while phi <= math.pi:

            x = r*math.cos(theta)*math.sin(phi)   # xyz coordinates
            y = r*math.sin(theta)*math.sin(phi)
            z = r*math.cos(phi)

            # (x-Rs)**2.0 + y**2.0 + z**2.0 = Rs**2.0

            if (x-Rs)**2.0 + y**2.0 + z**2.0 > Rs**2.0:  # For points within large sphere....
                                                          # .....and outside small sphere
                Dx = x - Rs        # vector from infinitesimal mass to center of small sphere
                Dy = y - 0.0
                Dz = z - 0.0

                D = math.sqrt(Dx**2.0 + Dy**2.0 + Dz**2.0)  # distance from mass dm to small sphere center

                dV = (r**2.0)*math.sin(phi) * dr * dtheta * dphi  # infinitesimal volume

                dm = rho * dV # infinitesimal mass

                dU = G*Ms*dm/D # infinitesimal potential energy contribution

                U = U + dU  # update total potential energy value

            phi = phi + dphi
            count = count + 1

            if count%10**6 == 0:
                print count/10**6

        theta = theta + dtheta

    r = r + dr

##########################################

print ""
print ""
print U/U_ref

Steven Chase - 1 year, 9 months ago

Very nice , thx a lot Sir

Kudo Shinichi - 1 year, 9 months ago

@Steven Chase Sir have a look at this interesting problem .

Kudo Shinichi - 1 year, 10 months ago

I think I would use a triple integral and a computer to solve this

Steven Chase - 1 year, 10 months ago

Sir , can u give some intial steps to proceed this problem ?

Kudo Shinichi - 1 year, 10 months ago

@Kudo Shinichi – Do you know what the answer is supposed to be? I would like to check my numerical result, once derived.

Steven Chase - 1 year, 10 months ago

@Steven Chase – Yeah sure , Sir. Very sry for late reply

Kudo Shinichi - 1 year, 9 months ago

@Kudo Shinichi – What is the expected result?

Steven Chase - 1 year, 9 months ago

@Steven Chase – Sir i think it should be close to GM^2/8R

Kudo Shinichi - 1 year, 9 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$