Non-trivial equivalent resistance.

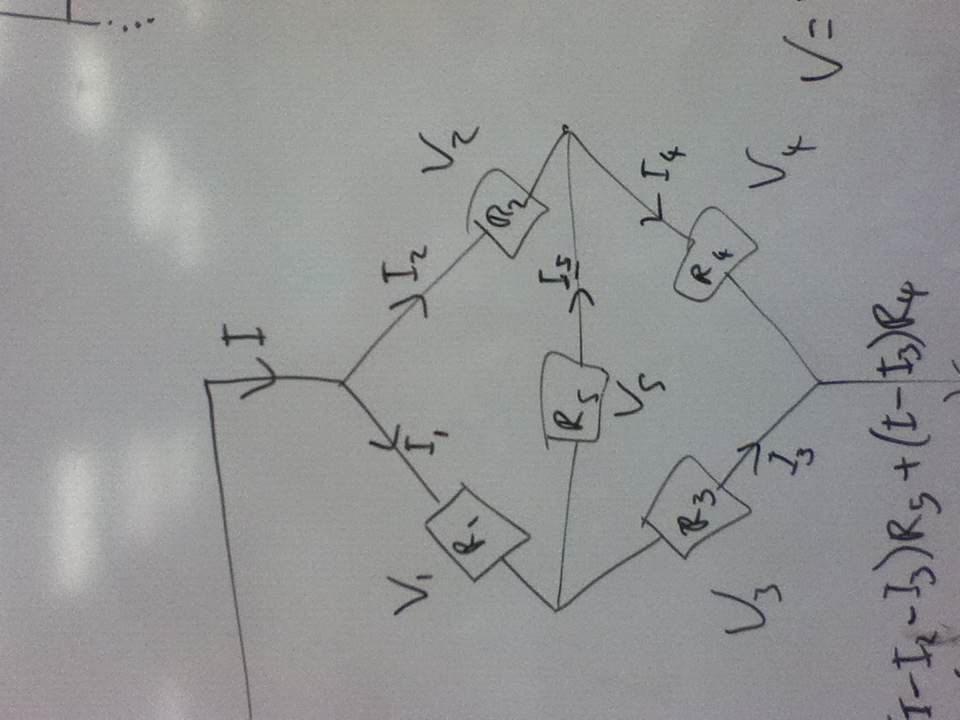
At school we have been learning the rules for equivalent resistance in series and parallel (which I covered at least two years ago, so I'm bored) and I asked my teacher about the circuit shown, which cannot be decomposed into a collection of series and parallel circuits.

I spent most of a lesson just bashing it with algebra, and in the end I found a three-line fraction for $R_{eq}$ in terms of $R_{1}$ , $R_{2}$ , $R_{3}$ , $R_{4}$ and $R_{5}$ .

So I was wondering: is there a nice method?

#Algebra #AlgebraicManipulation #ElectricityAndMagnetism #Resistance #Bash

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

I think delta - star method can help .

Keshav Tiwari - 6 years, 7 months ago

Can you give me an explanation/link to an explanation? Thanks

Sophie Crane - 6 years, 7 months ago

@Sophie Crane It's trivial using Y- $\Delta$ transformation. Just apply this on any of the ends of $\text{R}_{5}$ .

Ishan Singh - 6 years, 6 months ago

@Ishan Singh – Thank you very much. This is an excellent technique and I had never heard of it before. Awesome! :D

Sophie Crane - 6 years, 6 months ago

If u use loop rule instead of junction rule, the expression would have been simpler. For making it even simpler u can assume the circuit to be connected across a good emf(I mean u can take different emfs if values of the resistances are known)

Aneesh Kundu - 6 years, 7 months ago

I used both. The emf is an arbitrary value. All resistances are unknown, and are to be treated as algebraic variables. I am trying to find a general expression for the equivalent resistance in terms of these variables.

Sophie Crane - 6 years, 7 months ago

That would be a very big formula

Aneesh Kundu - 6 years, 7 months ago

@Aneesh Kundu – It is. That's why I posted this.

Sophie Crane - 6 years, 7 months ago

But u can still assume any value for emf as that wouldn't change the equivalent resistance.

Aneesh Kundu - 6 years, 7 months ago

Correct me if I'm wrong, but isn't this the outline of a Wheatstone bridge? If $\dfrac{R_2}{R_4}=\dfrac{R_1}{R_3}$ , then the equivalent can be easily calculated since the resistance $R_5$ will be ineffective. Is that condition given, or the variables $R_1,R_2,R_3,R_4,R_5$ can have any positive real value?

Prasun Biswas - 6 years, 6 months ago

You are correct on every count. The condition is that the resistors can take on any positive real value.

Sophie Crane - 6 years, 6 months ago

I got a fraction of 8 terms over 4 terms

Mohamed Ashraf Mostafa - 6 years, 6 months ago

Did you use delta-wye or something else?

Sophie Crane - 6 years, 6 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$