Nonconducting nonuniform non-nonsymmetric cylinder

A long, nonconducting, solid cylinder of radius 4.0 cm has a nonuniform volume charge destiny pp that is a function of radial distance rr from the cylinder axis: p=Ar2p=Ar^2. For A=2.5μ/m5A=2.5 \mu /m^5, what is the magnitude of the electric field at (a) r = 3.0 cm and (b) r = 5.0 cm?

So, clearly, I overdid it. See #2 for a legible version of solution to (a). For me, apparently, that was step one. So now the question is, WHAT ABOUT REPULSION? See below, the concentric circles on top right:

For every differential excerpt drdr, the enclosed charge qencq_enc generates an electric field perpendicular to the circumference. This field points both ways - outward and inward. Now, don't inward electric field lines of r+drr+dr cancel those of rr and form a certain EnetrE_{net_{r}}?

At first, I've tried to formulate an integral based on Er−Er+drE_r - E_{r+dr}. You can imagine how that went (∫...(r+dr)dr\int ...(r+dr)dr...). Then, I thought instead I should do Enet=Er−ER−rE_{net}=E_r-E_{R-r}. It led to the circled big formula , derived after an hour of globbling - above.

Something was wrong. This equation is clearly not elegant. And when physics throws you an elegant problem, you must get an elegant answer. Then I realized something... do you know what it is? It made me mad. I'll leave it to you to figure out ;)

NOTE Spoilers ahead! If you don't know the answer to above, give it a thought!

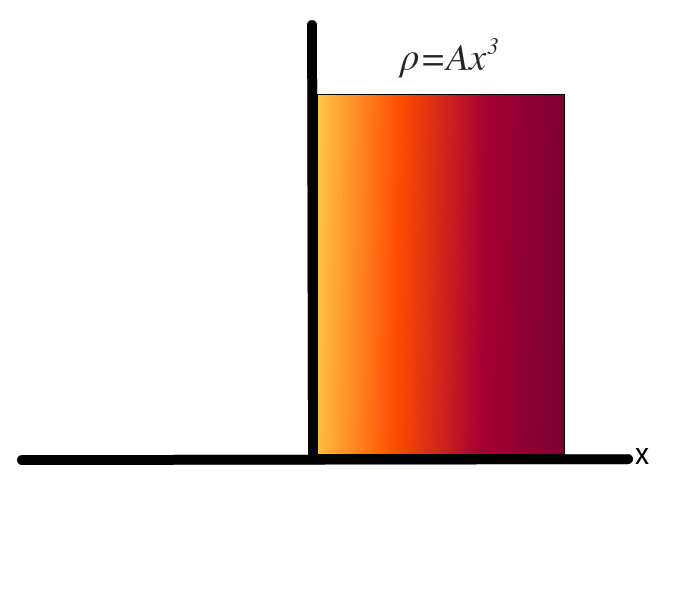
So, what if we DID have to resort to such measures? What if there was no internal symmetric cancellation? How would we resolve that issue? Say, for example, we have a big rectangle - and its charge density obeys the same pattern as that cylinder. If we place the rectangle on origin with length parallel to y axis, let rr be xx. What would be its electric field lines (assume it's infinitely long)? NOW my issue is real.

#ElectricityAndMagnetism

Note by John M.
6 years, 2 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

There are no comments in this discussion.

×

Problem Loading...

Note Loading...

Set Loading...