Number Theory Problem
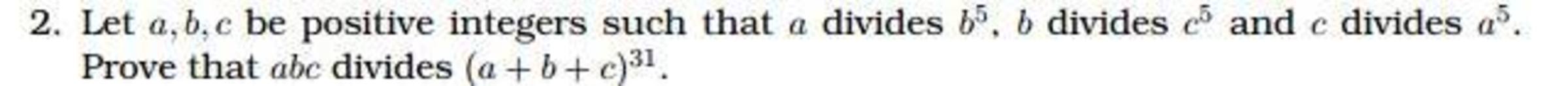
Can someone please help me with the following question
It first appeared in RMO 2012
No vote yet
5 votes
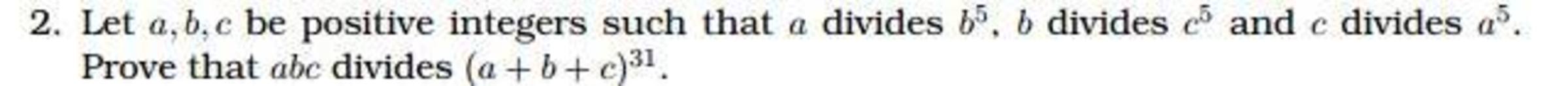
Can someone please help me with the following question
It first appeared in RMO 2012
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
Well, first of all we note that a divides c25: if b divides c5, then b5 divides c25. Because a divides b5, it divides also c25. This can be applied cyclically: b divides a25 and c divides b25.
In the factorization of (a+b+c+)31 there will be three members a31;b31;c31, members like n⋅ak⋅b31−k (and cyclical, i.e. others with ac or bc instead of ab) and members like abc⋅something. Clearly, abc divides all the members of the third type. We can express a31 as a25⋅a5⋅a, for the observation written above, it's dividible by abc.
Remains the second case:let's assume WLOG that's with the letters a and b.
We have three cases: k<5,k=5 and k>5.
In the first one, 31−k≥26, so we can express ak⋅b31−k as akcdotb25⋅bh where h is a positive integer. a divides ak, b divides bh and c divides b25 so abc divides ak⋅b31−k .
In the second case,ak⋅b31−k is a5⋅b21⋅b5. c divides a5, b divides b21 and a divides b5.
In the third case, we can express ak⋅b31−k as a5cdotaj⋅b31−k where j is a positive integer. c divides a5, b divides b31−k and a divides aj. Q.E.D.
A better solution would be choose any prime p dividing a,b,c and consider the maximum powers of p in a,b,c respectively α,β,γ and WLOG let α≥β≥γ .Now the max power of p dividing (a+b+c)31 is p31γ .It suffices to show that α+β+γ≤31γ but α≤5β≤25γ from the given condition.So summing them we get the desired inequality.This helps an easy generalization: let a,b,c be natural numbers such that a∣bn,b∣cn,c∣an then abc∣(a+b+c)n2+n+1