Not go on the title, in this discussion I will not deal with percentage but instead measure of area
In the below diagram \(O\) is the center of the circle with tangents \(\overline{BD}\) and \(\overline{AE}\)
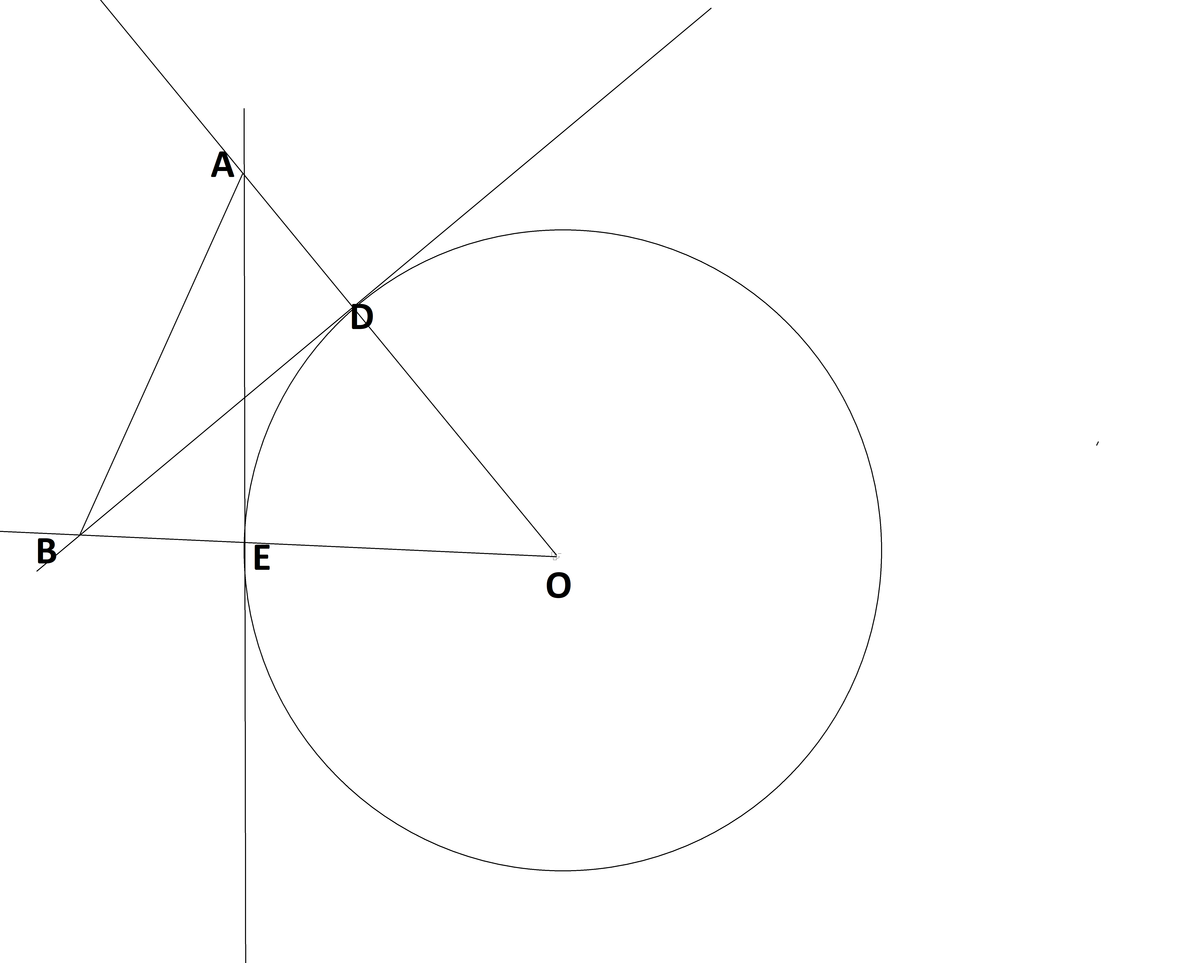
The area of △AOB=21OD2tan(∠AOB)sec(∠AOB)
Proof:
Let OD=x;∠AOB=θ
In △AEO
tan(θ)=xAE
AE=xtan(θ)........[1]
As ∠AEO=90°, applying Pythagorus theorem
x2+AE2=AO2
AO2=x2+x2tan2(θ)=x2(1+tan2(θ))=x2sec2(θ)
AO=xsec(θ)........[2]
Now in △AEO and △BDO
∠AEO=90°=∠BDO
∠AOE=θ=∠BOD
OE=x=OD
From RHS criterion of congruence
△AEO≅△BDO
∴AO=BO........[3]
Area of △ABO=21BO×AE
From [3] and this
Area of △ABO=21AO×AE
From [1],[2] and this
Area of △ABO=21xsec(θ)×xtan(θ)=21x2tan(θ)sec(θ)
Bonus
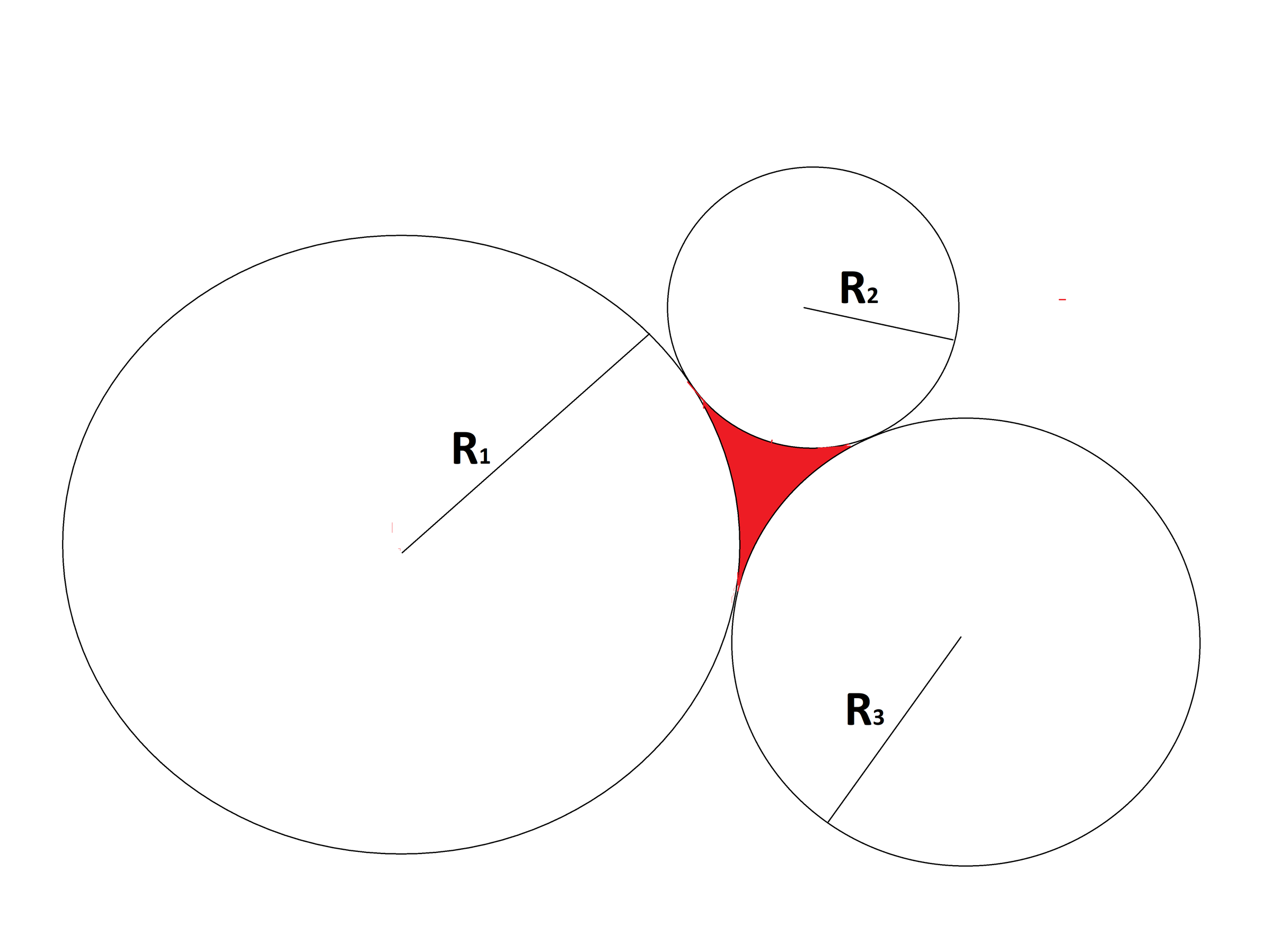
In the above diagram if you know the value of R1,R2 and R3, then find a formula to find the area of the red region.
Note:
- I myself don't know the answer to the bonus problem.
#Geometry


Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
@Zakir Husain,I will try to find shorter method.
Log in to reply
Or try writing it out as one formula and try to factorise & simplify :)
If someone gets the answer with solution of bonus, please share! Thanks!
@Mahdi Raza,@Zakir Husain,@Jeff Giff
Log in to reply
Incredibly! long formula
Log in to reply
Ya,the earlier solution is longer than it.I'll try to short the formula
Can you describe the parts of this formula? Did you "use Heron's formula and then try to subtract the sectors"... If so I think there is a small mistake in Heron's formula, it's: s(s−r1)(s−r2)(s−r3). Anyways please describe how you got till this formula. Thanks!
Log in to reply
@Mahdi Raza,check my solution
Wait…but the triangle’s sides aren’t r1,r2,r3, and it is equilateral (tangent of circle from same point)
It might be the smallest among the radii of the circles, but we need more proof. :/
@Jeff Giff, @Mahdi Raza, @Kriti Kamal - the red area is not a triangle so don't confuse, it is a shape made of three arcs not three sides.
Log in to reply
Yes, but I meant the smallest triangle containing the red area :)
I have considered them as arcs not as linesegmets :-)
Oic. My solution is different. I thought about the smallest triangle containing the red area :)
So my solution is sizeof△containing red area −sizeofARCH1,2,3
Log in to reply
Maybe I am wrong :D Sorry for being unhelpful :|
Log in to reply
See my solution..
@Zakir Husain,@Mahdi Raza,@Jeff Giff,
Log in to reply
A good explanation!. Any other formula? @Justin Travers, @jordi curto, @Yajat Shamji, @Kumudesh Ghosh, @Alak Bhattacharya, @Vinayak Srivastava, @Aryan Sanghi, @Marvin Kalngan.
Log in to reply
The angles can be calculated in sin inverse and cos inverse function
@Zakir Husain,can i send another version of solution
Log in to reply
Sure!
The area of the triangle can be found using Zakir’s formula above:
Or any x and θ pair with the relation above.
Log in to reply
You are assuming that the perpendicular of AB at point D will touch the point C, the same assumption you have to make to the perpendicular of AC and point B. Then only you can apply my formula to get the area of △ABC. You first have to prove that these assumptions are true for all cases. Or you can build a new formula for this special case separately.
Aha! @Zakir Husain, your formula can be simplified as 21x2sinθ, since tanθsecθ=tanθcosθ1=cosθcosθsinθ=sinθ :)
Log in to reply
tanθsecθ=cosθsinθ×cosθ1=cos2θsinθ
Log in to reply
Oops!
Slight improvement: express angles in radians. Then, the formula becomes sr1r2r3−cyc∑r12tan−1sr1r2r3
Log in to reply
I know it.but generally i use my most of work in degrees