===Open Problem #1=== (2nd Update Post)

Final push! I'm going to declare next week the final full week of Open Problem #1, and post Open Problem #2 on December 11th.

Please compile any information at the wiki here. After December 11th I'm going to forward what we've found to the mathematician (Erich Friedman) who posed the problem in the first place.

To reiterate, here is our open question. There is currently no known answer in the finite case.

On a chessboard of any size, is there a configuration of kings and knights such that each king attacks exactly 2 kings and 2 knights, and each knight attacks exactly 2 kings and 2 knights? Also, what's the smallest board needed?

WIKI PAGE DEDICATED TO THE PROBLEM; WE CAN COLLECT OUR DATA HERE

Source.

Details: Kings can attack any adjacent square, including diagonally. Knights move in an L shape as shown below.

Recent highlights:

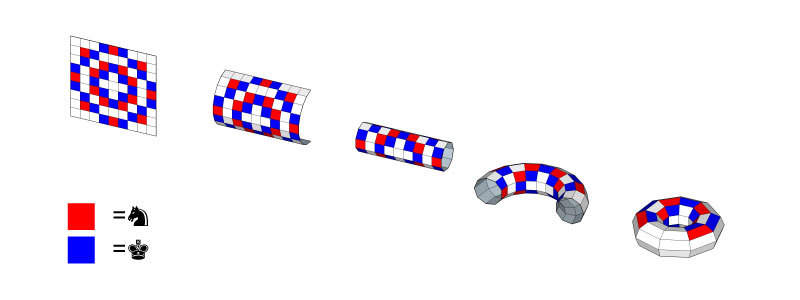
Stefan Van der Wall came up with a solution on a cube and Sizheng Chen posted a solution on a torus.

Ahmed Amrani wrote a computer program checking all cases from 5x5 to 17x17, with no solution.

Still possible routes of study:

A complete description of all possible king configurations on a finite board. The current data is on the wiki here.

Studying restrictions to configurations when they are on the side of the board or in the corner of the board.

Ahmed Amrani's program can be used to check cases larger than 17x17.

Thank you everyone for your efforts so far!

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

To whom it may concern: when I was working on this challenge, I created some code in Python where you can put in a board with a few pieces, and it would automatically add as many pieces as possible to the board. I used it to double-check multiple pieces of the work done on this challenge, but I was never able to make any new discoveries. I forgot to post it, so better late than never I suppose. Maybe somebody else will find it useful. I hope it's commented well enough and prints enough to be understandable.

Link to the Python code

Stefan van der Waal - 3 years, 5 months ago

@Jason Dyer What type of problems are allowed in the Open Problem #2?

Munem Shahriar - 3 years, 6 months ago

Go to the Thread for Suggesting Open Problems. It has guidelines and you can post your suggestions there.

Link to thread

Jason Dyer Staff - 3 years, 6 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$