===Open Problem #3===

Welcome to Open Problem #3! This problem is rather different than the last two, so if you haven't jumped in yet, now is a very good time to do so! You'll find artistic imagination to be just as useful as mathematics.

It's possible to design a polygonal billiard table such that there are two points that can never connect with one "shot". That is, it's possible to set up a ball in one place and a hole at another such that if the ball is hit once and reflects and unlimited number of times, it will never reach the hole.

(This assumes geometric purity: the "ball" has no mass and the "ball" and "hole" are considered single points. Also, if the ball hits a vertex point as opposed to a side then the reflections are absorbed.)

This has been done with a 26-sided table and a 24-sided table. However, it is unknown if 24 sides is the minimum.

Problem #1: Make a different billiard table that fulfills the above conditions, with any number of sides.

Problem #2: Either prove that 24 sides is the minimum or provide a counterexample.

Problem #1 should be considered truly open $-$ there aren't many examples, and creativity is encouraged, even if the number of sides is high.

In addition to tackling the problems above, an excellent contribution to this project would be to make a computer program that allows playing with different configurations and seeing what happens with the reflection.

In order to make it easier to post solutions, I've rendered Problem #1 as a problem to solve in the group. Post any images you might create there.

Before you start, you should study the example below, which was the first given to show that that the no-reflections-pair setup with a polygon was possible.

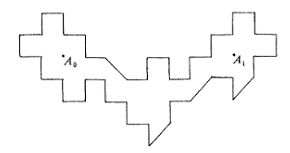
It comes from a paper by George W. Tokarsky. The proof is fairly short, but requires an intermediate proof.

Lemma: Prove that, starting at the marked vertex of the billiard table shown (shaped like an isosceles triangle), it is impossible to hit a ball that reflects back to where it started (given any number of reflections).

I've posted this as a problem to solve.

Knowing the Lemma, this proof then follows:

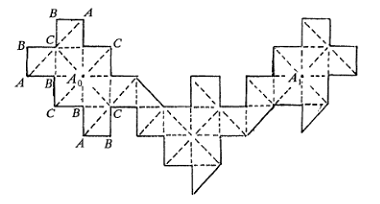
If there were a pool shot from $A_0$ to $A_1 ,$ the initial path must pass through the interior of one of the eight triangles surrounding $A_0 .$ Let us call this triangle $T.$ As in the lemma, a pool shot from $A_0$ to $A_1$ would correspond or fold up to a pool shot from $A_0$ to $A_0$ of $T,$ which is impossible.

Update: I highly recommend checking this solution from David Vreken which includes some new diagrams that work and explain a general method.

Quick update on Open Problem #2: I have rendered the text from the proof the group made into a PDF file suitable for publication, using the official American Mathematical Society format. I'm going to make a few review passes first before posting it.

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

We're mentioned in Numberphiles video !

conrad crowley - 3 years, 4 months ago

For problem 1, a simple solution will be that of a circle with a hole in the center and the starting position anywhere else on the circle. Unless the ball is shot directly into the hole, the ball would not enter the hole. Is this allowed?

Julian Poon - 3 years, 5 months ago

Our problem is specifically with polygonal tables. When curved sides are allowed we can get entire chunks of the table that can't reach each other.

Jason Dyer Staff - 3 years, 5 months ago

I know a better solution, make a figure 8 table and the ball won’t be able to go to the other side of the table 😎

Lee Isaac - 3 years, 4 months ago

Anyways, if you shoot the ball directly away from the hole, it would bounce and go in, as it would hit at a perpendicular angle.

Charlotte Poracchia - 3 years, 1 month ago

"(This assumes geometric purity: the "ball" has no mass and the "ball" and "hole" are considered single points. Also, if the ball hits a vertex point as opposed to a side then the reflections are absorbed.)"

So no, it won't work.

Steven Jim - 3 years, 1 month ago

On the computer software side of things, I might have a shot off programming something at the weekend. I found this if anyone wants to play around with the 26-gon. Wolfram

conrad crowley - 3 years, 5 months ago

Looks promising!

Jason Dyer Staff - 3 years, 4 months ago

It does not need to be a regular polygon, right?

Gustavo Acco - 3 years, 5 months ago

Correct. (The examples given definitely are not.)

For some reason I couldn´t see the examples before, thank you!

@Gustavo Acco – Espescially study what's going on with the last picture -- once you figure it out, it isn't too hard to make your own. (It's hard to make one with less sides than 24, though!)

I think we should definitely be able to connect the two points with a single shot in a regular polygon.

Akeel Howell - 3 years, 4 months ago

Is the lemma also valid for a non-right isosceles triangle?

Nevermind it definitely doesn't hold in the case of a equalateral triangle.

Could you post ("Is this valid for a non-right isosceles triangle") that as a problem in the group? (Then set the solution to "no" and you can your solution there if you like.)

@Jason Dyer – Then we can shoot along one of the sides! It doesn’t violate the “Also, if the ball hits a vertex point as opposed to a side then the reflections are absorbed” rule!

Steven Jim - 3 years, 5 months ago

@Steven Jim – Sorry I don't understand how you can deduce shooting along the sides from it not holding for non right isoceles triangles

@Conrad Crowley – Sorry for late response. And never mind, I misunderstood.

Steven Jim - 3 years, 4 months ago

If you shoot the ball straight up, shouldnt it return?

Philip Kalisman - 3 years, 4 months ago

No as it hits the vertex. The problem states that if the ball hits a vertex reflections are absorbed.

Now it does

@Jason Dyer I’m not sure what you have on problem 2, but I have a counter example of 21 sides and an almost complete sketch for a proof of minimality. Please let me take a look on that pdf of yours :)

Bernardo Picão - 2 years, 4 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$