Ortho-circumcentric complexity

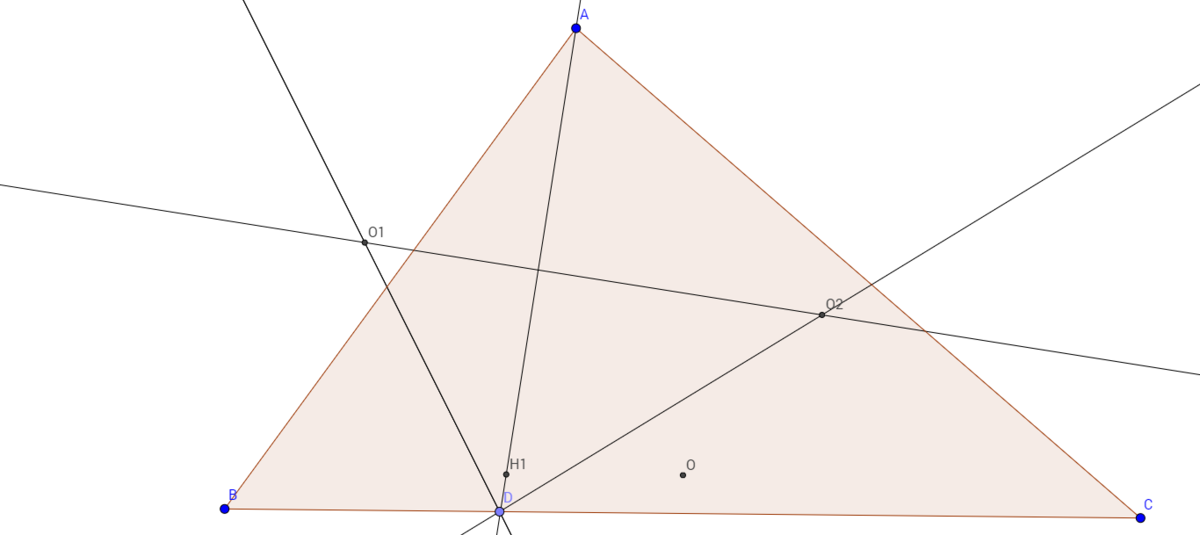
Consider an acute-angled triangle $ABC$ , with circumcenter $O$ .

Denote the point $D$ such that it lies on segment $BC$ .
Let $O_{1}$ and $O_{2}$ be the circumcentres of triangle $ABD$ and $ACD$ , respectively.

Consider the triangle $O_{1}O_{2}D$ , with orthocenter $H_1$ .

Prove that: $O H_{1}$ is parallel to $BC$ .

Bonus: Prove this result for an obtuse-angled triangle as well.

#Geometry

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

For a general triangle $\overline{ABC}$ , we define $p_{ij}$ to be the perpendicular bisector of the two points $i$ and $j$ , and $h_{ij}$ to be the altitude of the triangle corresponding to the line through two points $i$ and $j$ of said triangle. So, the perpendicular bisectors $p_{AB}$ , $p_{AC}$ and $p_{BC}$ are perpendicular to $AB$ , $AC$ and $BC$ respectively and all meet at the circumcentre $O$ of $\overline{ABC}$ . For a point $D$ on $BC$ , we may suppose that $O_1$ and $O_2$ are the circumcentres of $\overline{ABD}$ and $\overline{ACD}$ . We then have that $O_1$ and $O_2$ are respectively the meets of the concurrent triple of lines $(p_{AB},p_{AD},p_{BD})$ and $(p_{AC},p_{AD},p_{CD})$ . As $p_{AD}$ passes through both points, we can deduce that $p_{AD} = O_1O_2$ . For the triangle $\overline{O_1O_2D}$ , we then have that the altitude $h_{O_1O_2}$ of this triangle is simply $p_{AD}$ ; this then implies that the orthocentre $H_1$ of $\overline{O_1O_2D}$ lies on $AD$ . It remains to show that $H_1O$ is parallel to $BC$ .

I will get back to you on this, as I will need a couple more days to work this out.

A Former Brilliant Member - 2 years, 9 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$