Orthocentre distance to triangle vertices as a function of triangle angles and side lengths.

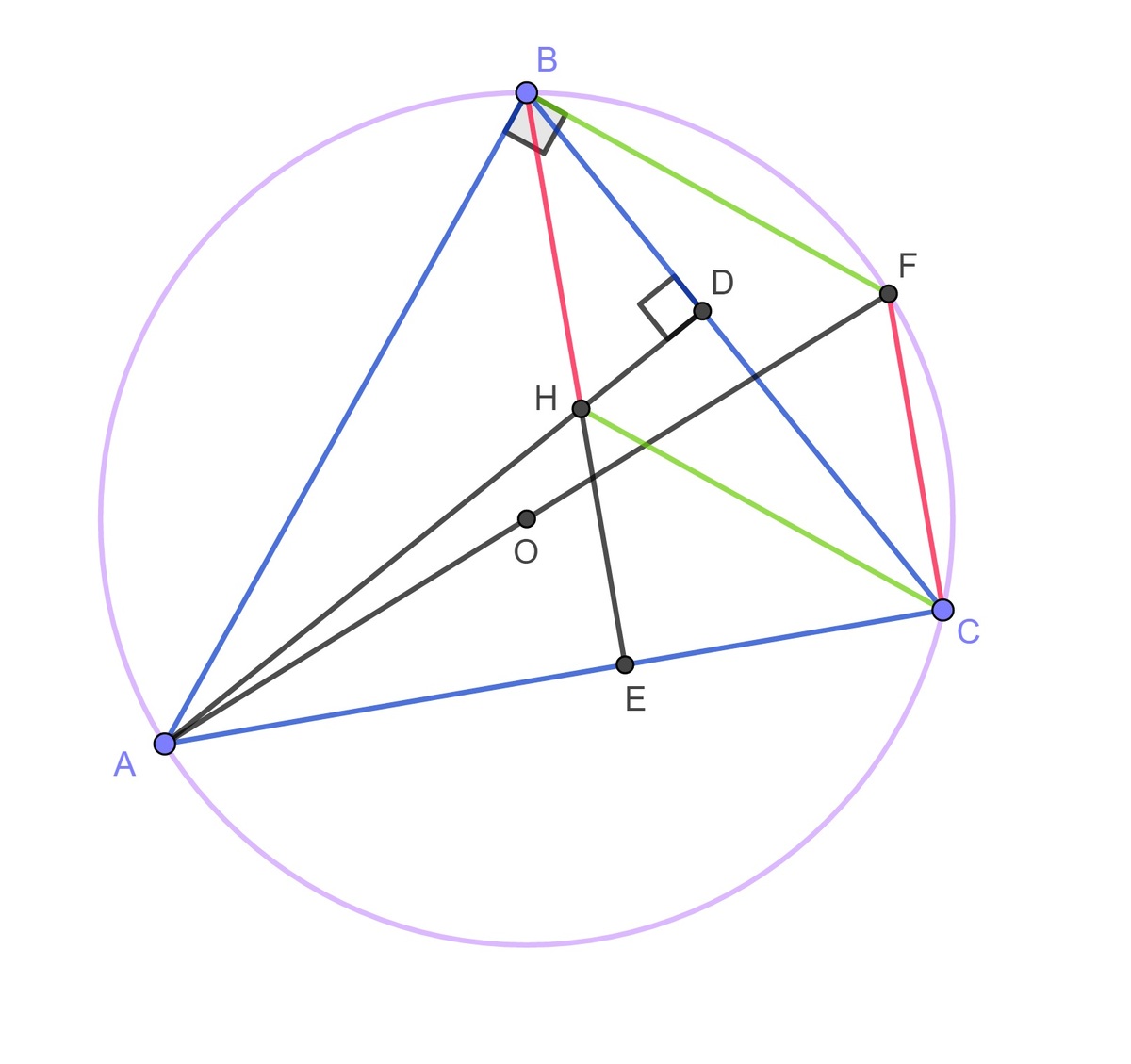
While solving one of Brilliant problems I came across an interesting property of an orthocentre which I have not thought of before, so I decided to share it with Brilliant community. Let's consider a triangle $ABC$ with circumcentre $O$ , orthocentre $H$ , radius $R$ , $AB=c, AC = b, BC = a$ . Let's create circumcircle with diameter $AF$ and connect points $BF$ . $BF \perp AB$ (from Thales' Theorem) and $CH \perp AB$ ( $CH$ is part of the altitude of the triangle) $\Rightarrow BF \parallel CH$ . For the same reasons we can state that $CF \parallel BH$ . This means that quadrilateral $BFCH$ is a parallelogram and $BF=CH$ and $CF= BH$ . It is also follows from Inscribed Angle Theorem that $\angle BFA = \angle ACB$ and $\angle AFC = \angle ABC$ . $BF = 2R \cos(\angle BFA ) = \dfrac{AB}{\tan(\angle BFA)} \Rightarrow$ $CH = 2R \cos(C) = \dfrac{c}{\tan(C)}$

For the same reasons the following holds true: $AH = 2R \cos(A) = \dfrac{a}{\tan(A)}$ $BH = 2R \cos(B) = \dfrac{b}{\tan(B)}$

Because of special cases for right angles, It is better rewritten as: $AH = 2R \cos(A) = a \times \cot(A)$ $BH = 2R \cos(B) = b \times \cot(B)$

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Some criticisms:

You will need to expand on your proof. Specifically, say that $BF \perp AB$ because of Thales' theorem and that $CH \perp AB$ , since the line joining CH is an altitude of the triangle $\overline{ABC}$ through $C$ .
What is $R$ ? Please define your terms precisely. I will also make the same argument with the upper-case and lower-case $a$ 's, $b$ 's and $c$ 's... are they points? Angles? Distances?

All in all, an unclear proof to an interesting but probably well-known result (I do not think this is new, though; this would be something that was well-known to probably Euler or Monge, but I would have no clue on the historical context). I would be interested to see if this result generalises to arbitrary dot product geometries.

P.S. If I find a result in the rational analog for not only the triangle but also the tetrahedron, I'll be sure to credit you!

A Former Brilliant Member - 2 years, 10 months ago

The symbols are commonly used as a standard, but I added the information. The very reason I wrote that note is that I have not seen that information before. I am not claiming it is new. Most likely it is not. It is for the information for other members of Brilliant. It is nothing advanced, rather simple, but could be useful in some instances. I was not going for a strict proof, rather sketchy one. Just sharing information with others. For more information on orthocentre properties you can also check my solution for problem

Maria Kozlowska - 2 years, 10 months ago

No worries. I am currently finishing my thesis in three-dimensional rational geometry, but when I’m done I have two papers to write on tetrahedron centres in rational geometry. Will have a look at your stuff when I’m onto it.

Wow ! That's pretty cool . Please keep up the good work 😀

MEGHNA SINGH - 2 years, 1 month ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$