Parabola vertex proof

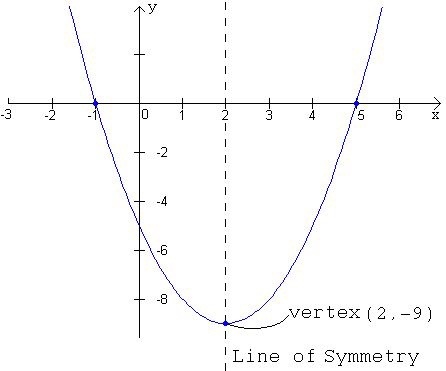
Yay, my first note!! In this note, I will discuss the rather simple proof of a parabola's vertex equation being $x=\frac{-b}{2a}$ , I couldn't find it anywhere on brilliant so I figured I may as well post it.

We start with the standard parabola equation $y=ax^2+bx+c$ . Next, we take the derivative of this equation $\dfrac{\text{d}}{\text{d}x}y=ax^2+bx+c\Rightarrow2ax+b$ .

Now, a special property of the first derivative is that its roots occur at the same x coordinate as its antiderivatives's relative maxima/minima. Thus the vertex of a parabola will occur when $2ax+b=0$ . Solving for x, we get $x=\dfrac{-b}{2a}$ .

#Algebra #Calculus #Parabola #Proofs #Easymoney

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

why did u finded roots of the equation from which this general equation is made to come out from ? reply please

M Siddiqui - 6 years, 10 months ago

If you find the roots of the first derivative, it will yield the x coordinate of the minima/maxima of a function, in the

Trevor Arashiro - 6 years, 10 months ago

In the case of a second degree polynomial,c it will yield the vertex.

Trevor Arashiro - 6 years, 10 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$