Pascal's Triangles
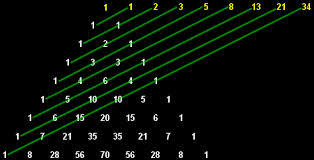
What interesting properties of Pascal's Triangle do you know?
Above see one of them: The Fibonacci Sequence.
No vote yet
1 vote

What interesting properties of Pascal's Triangle do you know?
Above see one of them: The Fibonacci Sequence.
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
The sum of the numbers in any row is equal to 2 to the nth power or 2n, when n is the number of the row. For example:
20=1
21=1+1=2
22=1+2+1=4
23=1+3+3+1=8
24=1+4+6+4+1=16
Log in to reply
That is quite natural because rth element of nth row of pascals triangle is nCr and sum of all those elements is equivalent to binomial expansion of (1+1)n or 2n.
Also, 2n is equivalent to number of subsets of a set and vertices of n dimensional hypercube. Look at the diagrams of lattices based on inclusion operation, They form hypercubes.
Basically, pascal's triangle, hypercubes in n-dimensions, binomial coefficients, power sets and their lattice and recurrence relation [T(n)=1+Sum of all previous elements {with T(0)=1}] are all related. Maybe i'll post all of their relations that i know with corresponding images sometime later.
I know another property:
If in the row n the second number is prime, all numbers in this row except the 1s on the sides, will be multiples of this number.
Examples:
Row 7:
172135352171
7 is a prime and 21 and 35 are multiples of 7.
Row 17:
1171366802380618812376194482431024310194481237661882380680136171
17 is prime and 136, 680, 2380, 6188, 12376, 19448 and 24310 are multiples of 17.
Log in to reply
Cool
If you color the odd numbers in Pascal's triangle black, you get Sierpinski's Triangle.
I think you can find all the terms in a Fibonacci sequence from any two, anywhere in the sequence, which you are given. Imagine you are told that 10 and 41 are the 5th and 9th terms.
... , ... , ... , ... , 10, a, b, c, 41, ... , ...
10+a = b a + b = c, which is 10 + 2a = c by substitution b + c = 41, which is 10 + a + 10 + 2a = 20 + 3a = 41 by substitution, therefore 3a = 21 a=7, b=17, c=24
29 , -16 , 13 , -3 , 10, 7, 17, 24, 41, ... , ... I filled in the first four terms by applying the rule in reverse.
Now in theory you will always have as many equations as unknowns in the section of the sequence with the given numbers at the start and end. I'm pretty convinced it works.
It is directly related to choosing (nCr) so it can be used for probability. For example if you look at flipping a coin, if you call moving down and left heads and down and eight tails (it doesn't really matter, its symmetrical). Say we want to know the probability that if I flip a fair coin 5 times, what is the chance I will get 4 heads and 1 tails? I look at the triangle and move down and left 4 times then down and right once which would land me on a 5 I believe. The choosing comes in here because you can choose 5 routes that will have 4 lefts and 1 right. And since probability is a percent or a fraction, we need a denominator. So the denominator is found by adding the whole row up, in this case 1,5,10,10,5,1 so if a fair coin is flipped 5 times, the chance it will land 4 heads and 1 tail is 5/32.
(x+y)n =[(1st term of nth row from top] xny0+[2nd term of the row]xn−1y1+....….....................[last term of the row]x0yn..
where the ones in the square bracket are the co-efficients
EXAMPLE
» elements of second row 1,2,1
(x+y)2 =x2+2xy+y2
» elements of third row 1,3,3,1
(x+y)3=x3+3x2y+3xy2+y3
Triangular numbers are made starting from one of the 1's on the third row. 1,3,6,10,15,21,28,36,45,55,66,78....... (n^2 +n)/2
it is infinite
3 a number is a sum of two number above them
The sum of the numbers in a row is 2 to the power of whichever row it is.
Another really cool thing is that you can use the triangle to test for primes. It would be really slow and not efficient because at large numbers the triangle becomes huge! But if we label each row starting with 0, then for any n, if the numbers in the nth row (not including the ones) are divisible by n, then n is prime. For example 3, 4, and 5. The rows without the ones are 3,3; 4,6,4; 5,10,10,5. 3 is divisible by 3 and therefore a prime. 4 is divisible by 4 but 6 is not there for 4 is composite. 5 and 10 are both divisible by 5 therefore prime again!
I love how it can make an approximate Spierski Triangle but I know someone already mentioned that. All in all, the pascals triangle is amazing. Has anyone investigated patterns in Pascal's tetrahedron or Pascal's simplex? Cause those would be interesting.
Log in to reply
After I do a little bit of reading on them (Pascal's Tetrahedron and Simplex), I'll let you know .Think we can share that too. Well a Note would do or a Wiki?
ARYΔ
if you go down each diagonal starting from the left, the (n+1) row is the summation of the nth row.
It is a table for all binomial equations.
Each row is eleven to the nth row, with the top row clearly being the 0th.
On two sides of Pascal's triangle is the repeating number 1.
some fibonacci sequences include 0 as well in the sequence? What is the justification?
Log in to reply
If you mean the sequence starting 0, 1,1,2, 3, 5 instead of 1, 1,2,3,5 it's basically the same principle. The first two numbers must be given (or at least two numbers must be given and you can work out the others wherever they are, in theory, I think, but we normally give the first two). Here the first version is Fibonacci 0,1... and the second Fibonacci 1,1... and only the position number of the terms changes. I find it intriguing that the quotient of consecutive terms in Fibonacci sequences, regardless of the first two terms unless they are 0, 0 will tend to phi, the Golden ratio.
-2, 7, 5, 12, 17, 29, 46, 75, 121, ... by the time you get to 121/75 it's pretty close
Log in to reply
This is a good method to find other variations of the Fibonacci Sequence.
the number corresponding to the line is sum of the number corresponding to it
The Vandermonde convolution. That is all.
we can find expansion of any two terms having power n for example if we consider 1) (a+b)^5 ANS now look at the pascal triangle 1 (for power 0) 1 1 (for power 1) 1 2 1 (for power 2) 1 3 3 1 (for power 3)
1 4 6 4 1 (for power 4) 1 5 10 10 5 1 (for power 5) << (we are considering this line for expansion) i.e [(a)^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+(b)^5]
Relates to combination(nCr)
the sum of the integers in each row is a power of 2.
How about (x-1)
Here is a problem on the properties of odd numbers and there placement in each row in the pascals triangle
Do try it!
Each line corresponds to a power of 11 ( a rule follows beyond 11^4)
Each diagonal has its own property: 1st - 1 2nd - ascending consecutive numbers from 2 3rd - triangular numbers from 6 4th - tetrahedral numbers from 20
so on and so forth.
The whole pattern triangle is symmetrcal
binomial coefficients
012362