Physics special relativity - Space time and paradoxes - quiz 5 query.
A space ship is trying to escape a laser beam that is shot at them by hiding behind an asteroid of length 1. The ship is of length 5/3 and so has to travel at 0.8c to hide behind the asteroid, so that in the asteroids frame, it fits perfectly in the shadow.
Set up
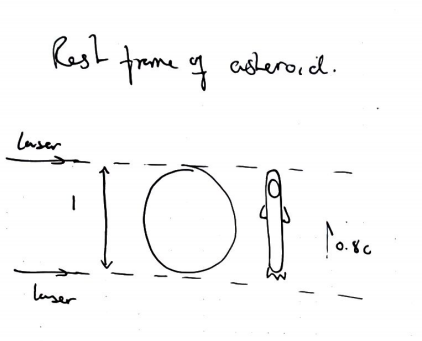
Call event A the rear of the ship entering the shadow of the asteroid and event B the nose of the ship leaving the shadow. Let event A happen at (0,0)
After applying the lorentz transforms it can be shown that event B happens 4/3 seconds before event A, in the frame of the ship.
The question asked is that, in the frame of the space ship, what fraction of it is left exposed as event B occurs, i.e when the nose leaves the shadow of the asteroid.
My reasoning is as follows, the asteroid has a length of 1 in its frame, and so has a length of 0.6 in the ships frame. The ship has a proper length of 5/3. The fraction left uncovered is given by 5/3−0.65/3. This is more than half.
This is the explanation given on the brilliant website:
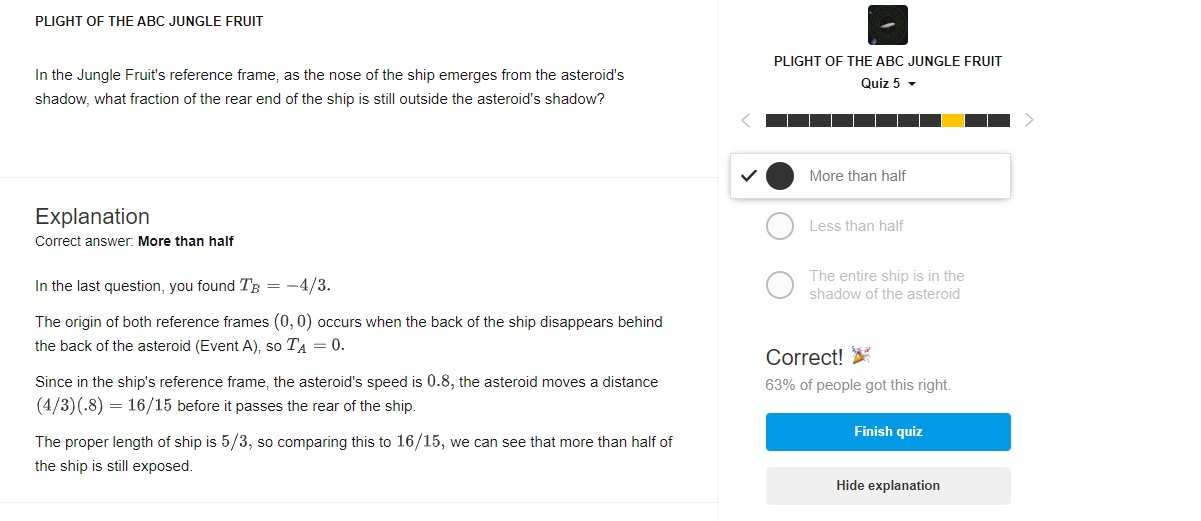
I dont understand why they are considering the distance travelled by the asteroid in the frame of the space ship ( the jungle fruit ). Can someone explain why my reasoning is incorrect.
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
There are no comments in this discussion.