Placing square on a grid - Part 3

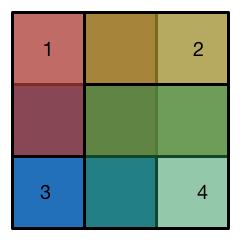
On a 3 by 3 grid, the red, yellow, blue and green 2 by 2 squares are placed in some order. They have to be placed in their location (IE not moved somewhere else). There are $4 ! = 24$ different ways to place these squares.

Of these 24 different ways, how many distinct results would we get?

For example, placing 1432 and 4132 will both yield

#Combinatorics

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

$16$ .

I'll be referring to the 2 X 2 squares as numbers, and each of the 9 squares as blocks. First, look at the four corner blocks. They can only be covered by the number on it. So we can disregard those. We are left with a central cross. The center of this cross can be covered in $4$ ways, since whichever number we choose first covers it. Now, we are left with the four other blocks. Of these, $2$ will be covered by the first number we chose, so they don't matter. We are left with two blocks. Each of these blocks can be covered by two numbers and each choice is possible, so we have $4 * 2 * 2 = 16$ .

Siddhartha Srivastava - 6 years, 2 months ago

I'm getting a total of $20,$ although your reasoning seems sound. As I understood the question the first number forms the bottom "layer", the second number the second layer and so on, so that the last number/color is on top. For the sequences that end in $23, 32, 14, 41$ it doesn't matter what the order of the first two layers is, so this produces $4$ duplicates. For the other $8$ possible pairs of top layers it will matter how the first two layers are chosen, so there are no duplicates here. Thus I get $24 - 4 = 20$ sequences that produce distinct patterns. Where is the flaw in my logic?

Edit: O.k., I see now. $1324$ gives the same result as $1234$ , $4321$ gives the same result as $4231$ , $3142$ gives the same result as $3412$ and $2143$ gives the same result as $2413.$ This gives us $4$ more duplicates, leaving us with $16$ distinct outcomes, as Siddhartha and Brock have found.

Brian Charlesworth - 6 years, 2 months ago

Wow, that's a nice analysis! It's certainly simpler than I thought it would be.

Calvin Lin Staff - 6 years, 2 months ago

Nice approach. I did it in a similar manner too :)

Chung Kevin - 6 years, 2 months ago

I'm finding $\boxed{16}$ , gentlemen.

Python 2.7:

from itertools import permutations
found = set()
class Grid():
    def __init__(self):
        self.grid = [['w']*3,['w']*3,['w']*3]
    def __str__(self):
        string = ''
        for row in self.grid:
            for color in row:
                string = string + color
            string = string + '\n'
        return string
    def paste(self,origin,color):
        for x in xrange(2):
            for y in xrange(2):
                self.grid[origin[0]+x][origin[1]+y] = color
position = {'r':(0,0),'g':(1,1),'b':(1,0),'y':(0,1)}
for colors in permutations('rgby'):
    grid = Grid()
    for color in colors:
        grid.paste(position[color],color)
    found.add(str(grid))
print "Answer:", len(found)

Brock Brown - 6 years, 2 months ago

Nice program, Brock. I can't argue with its output; the answer is indeed $16.$ :)

Brian Charlesworth - 6 years, 2 months ago

Thanks! :D

Brock Brown - 6 years, 2 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$