Please help me ASAP2:Again, tricky geometry 😅

So yesterday I came across a problem(with a problem :/)in a book like this-
$\text{There are angles} \angle AOB ,\angle BOC, \angle COD \text{on a plane}.$
Given that $OM,ON$ bisect $\angle AOB,\angle COD$ respectively, And that $\angle MON=50^\circ ,\angle BOC=10^\circ$ , as in the figure, find $\angle AOD.$
But there was NO picture! And I was thinking about how to solve it but realised the possibilities are too complicated, as the size of angle AOB may vary.
Given that every angle is smaller than 180 degrees and bigger than 0 degrees, how should I separate the possibilities? 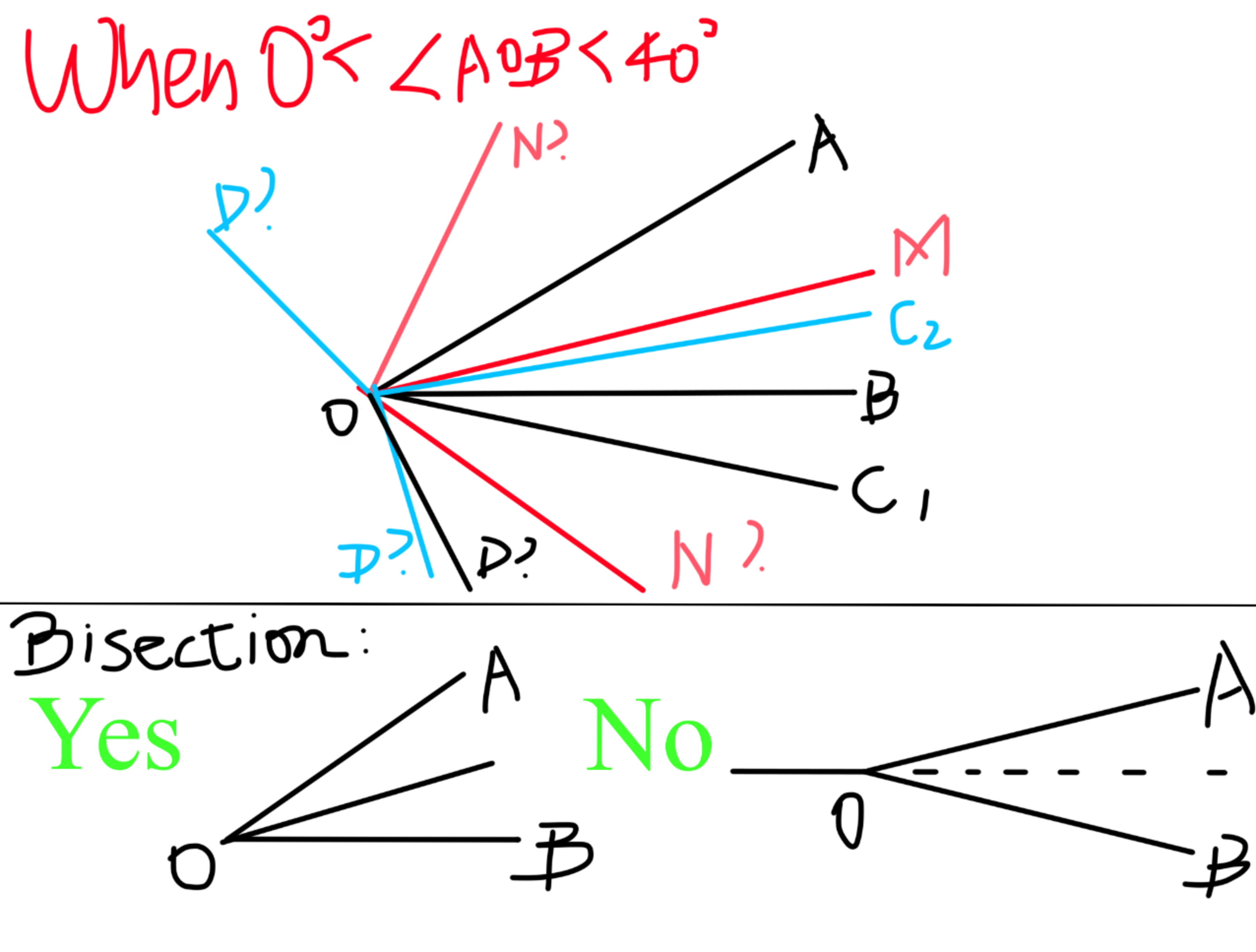one possibility

#Geometry

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Umm I should get to send the solution at the weekend, my maths teacher says I’m wrong and I still don’t know exactly why 😊

Jeff Giff - 4 months, 3 weeks ago

I'll ask my maths teacher to solve it.

Yajat Shamji - 4 months, 3 weeks ago

Geez guess what my maths teacher accidentally solved it wrong mwah hah hah :D

Jeff Giff - 4 months, 3 weeks ago

So I’m correct :P and I’m posting the solution

Jeff Giff - 4 months, 3 weeks ago

@Frisk Dreemurr

Jeff Giff - 5 months ago

@Jeff Giff, are you there?

I have got a solution for your question, but it'll take some seconds to send, alright...?

Frisk Dreemurr - 5 months ago

When I read this question, I decided to make a sketch of my own. So my first version was this: (angles and lengths both aren't to scale)

$50°$ is visibly the sum of the bisector of AOB, the whole BOC, and the bisector of COD

Subtracting only BOC to get the bisectors give $50° - 10° = 40°$ , which is the sum of BOM and CON

Multiplying it by two should give the sum of angles AOB and COD, which is $80°$

To get the value of AOD, we must add AOB, BOC and COD, which is $80° + 10° = 90°$

$\textsf{Hope you understood my explanation, I am not that good at explaining...}$ :)

Frisk Dreemurr - 5 months ago

thanks! That was part of my solution, but AOB might be bigger than 100 degrees, so MON could be inside AOB😅 not to mention that OC could be inside AOB, giving multiple answers😊

Jeff Giff - 5 months ago

But N must be part of ON, and according to the question, ON is the bisector of COD

Same goes to M and AOB

So AOB can not be bigger than $40°$

Frisk Dreemurr - 5 months ago

@Frisk Dreemurr – Look, in this possibility, AOB is bigger that 40 degrees :)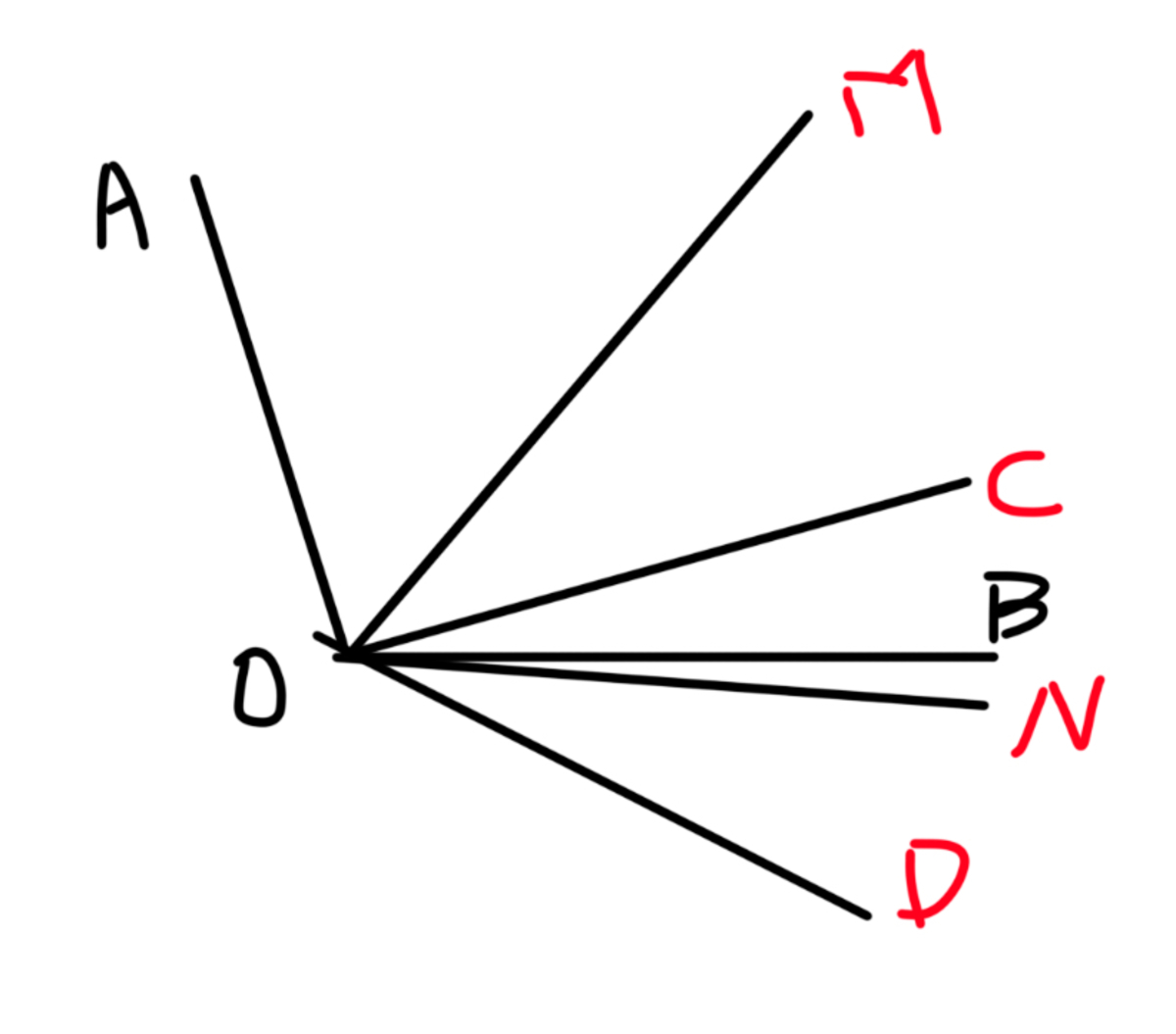

Jeff Giff - 5 months ago

@Frisk Dreemurr – BTW hamza, I solved it, with the size of AOB varying between 6 sections and OD with a total of 20 positions, BUT only two values of AOD. And since it was our homework, I’m going to show my solution to the teacher. I suppose I’m the only one to write a solution since they didn’t ask for one :)

Jeff Giff - 5 months ago

@Frisk Dreemurr – Wanna check out the solution? It would take a few minutes to send :)

Jeff Giff - 5 months ago

@Jeff Giff – Yes, why not?

As long as it is good, I'd love to see your solution :)

Frisk Dreemurr - 4 months, 4 weeks ago

Thanks a lot anyways, I hope to mention some more people but it turns out I can’t :P

Jeff Giff - 5 months ago

@Jeff Giff

Yajat Shamji - 4 months, 4 weeks ago

First, let $\angle CON=x^\circ$ .

Case 1

When $0^\circ \le \angle AOB \le 10^\circ$ so $\angle AOB$ is in $\angle BOC_1$ , as in the figure, there are 4 possibilities of AOD(the number after D shows the C and N it’s contributed by, e.g. $AOD_{11}$ matches with $C_1$ & $N_1$ ):
$\begin{aligned} \angle AOD_{11}&=\angle C_1OD_{11}-(\angle BOC_1-\angle AOB)\\ &=\angle C_1OD_{11}+\angle AOB-\angle BOC_1 \\ &=2x^\circ +2\angle MOB-10^\circ\\ &=(2x-10)^\circ +2(\angle BOC_1+\angle MON_1-\angle C_1ON_1)\\ &=(2x-10)^\circ +2(60-x)^\circ =\red{110^\circ};\\ \angle AOD_{12}&=\angle BOC_1+\angle C_1OD_{12}-\angle AOB\\ &=(10+2x)^\circ -2[10^\circ -(50-x)^\circ ]=\red{90^\circ};\\ \angle AOD_{21}&=\angle AOB+\angle BOC_2+\angle C_2OD_{21}\\ &=2(\angle MOB+\angle C_2ON_1)+10^\circ \\ &=2(\angle MON_1-\angle BOC_2)+10^\circ = 2\times (50-10)^\circ +10^\circ =2\times 40^\circ +10 ^\circ =\red{90^\circ} ; \\ \angle AOD_{22}&=C_2OD_{22}-\angle AOB-\angle BOC_2\\ &=2x^\circ -2\angle MOB-10^\circ \\ &=(2x-10)^\circ -2(x-50-10)^\circ =\red{110^\circ}. \end{aligned}$ -NOT FINISHED YET-

Jeff Giff - 4 months, 3 weeks ago

@Valentin Duringer here is a problem that can be included in dynamic geometry, because this is mad as the picture is not given, meaning we have to think of all 6 varieties of AOB and result in 20 AODs, which only return two values! :D It was my HOMEWORK and my maths teacher nearly said holy —— seeing my solution - didn’t realise what chaos would be caused without the picture :D

Jeff Giff - 3 months, 4 weeks ago

hum..chaotic indeed -)

Valentin Duringer - 3 months, 4 weeks ago

I’ll give the latex of the problem here later, copy it if you have time :)

Jeff Giff - 3 months, 4 weeks ago

CAREFULLY READ ASSUMPTIONS BEFORE CALCULATING
There are rods OA, OB, OC, OD(not necessarily ordered) on a plane. Given two rods OM, ON that bisect \ ( \angle AOB \ ) and \ ( \angle COD\ ) respectively, and that \ ( \angle MON =50^\circ ,\angle BOC =10^\circ \ ) , while the value of \ ( \angle AOB \ ) varies, find \ ( \angle AOD. \ )
Assumptions:
All angles are in range (0,\pi). That is to assure which side the angle bisector is on.
The size of AOB varies and so does the size of AOD. You will find a few finite possibilities for AOD. Input the product of all possible answers IN DEGREES as result.
e.g. if possible results are 10 degrees ,20 degrees and 30 degrees, then input 10\times 20\times 30 =6000 as your answer.

Jeff Giff - 3 months, 4 weeks ago

Just remember to add the latex brackets :)

Jeff Giff - 3 months, 4 weeks ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$