Plotting the Mandelbrot Set (Roughly)

Inspired by a recent problem by David Vreken.

The Mandelbrot Set is the set of complex numbers $c$ for which the following sequence does not diverge:

$\large{z_{n+1} = z^2_n + c \\ c = x + j \, y \\ z_0 = 0 \\ j = \sqrt{-1}}$

I found a divergence sufficiency criterion online:

#

The complex $c$ value has a magnitude less than or equal to 2
AND
Any sequence term has a magnitude greater than 2

#

Here were some other possible divergence sufficiency criteria discussed in the solutions section:

#

$x > 1$
OR
$y > 1$
OR
$y < -1$

#

Let's simply assume that these are right, and proceed with the following simulation:

1) Sweep through the $2D$ complex plane (varying $x$ and $y$).
2) Run 100 iterations of the sequence for each point to test the first divergence criterion
3) Apply the second set of divergence criteria as well
4) Plot points for which the sequence does NOT diverge

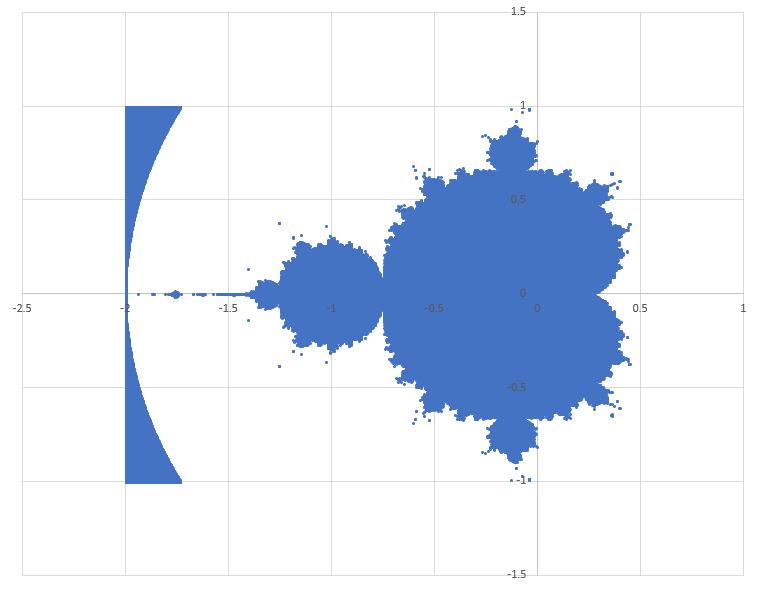
The result is shown below (plotted as an $x y$ scatter in Excel). Click to enlarge. It looks very much like the picture on the Wikipedia page, except for the anomalous portion on the left side. For some reason, the code didn't detect that those points diverge. Pretty cool, regardless. Code is attached below. Plots are included for both sets of divergence criteria combined (plot 1), and for only the first set (plot 2) (the ones I found online).

Plot 1 - Both sets of divergence criteria combined

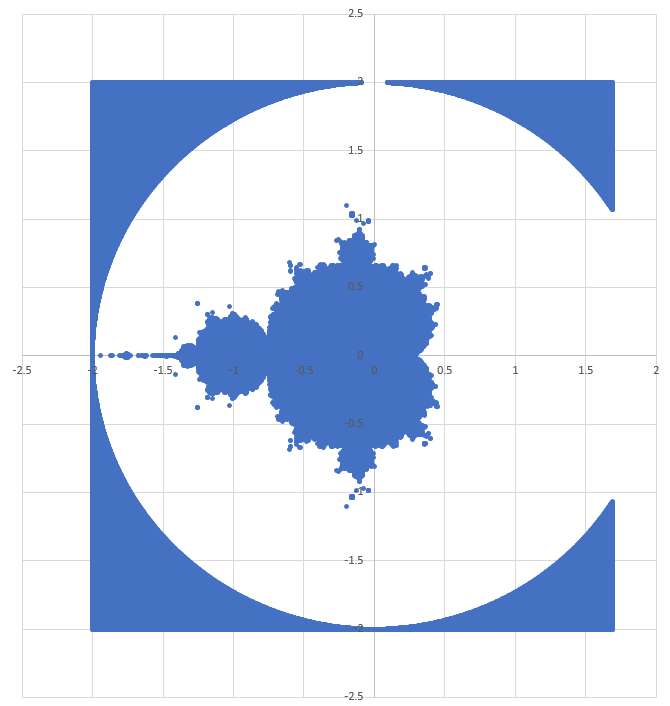
Plot 2 - Only the divergence criterion I found online

This one contains some more extraneous points around the periphery (outside a circle of radius 2).

Code (with full divergence-checking functionality):

import math

Nside = 2000
Nterms = 100

dx = 4.0 / Nside
dy = 4.0 / Nside

x = -2.0

while x <= 2.0:     # real part scan

    y = -2.0

    while y <= 2.0: # imaginary part scan

        c = complex(x,y)  # initialize values

        z = 0.0
        div = 0

        if abs(c) <= 2.0:  # apply first divergence criterion

            j = 0

            while (j <= Nterms) and (abs(z) < 10.0**6.0):

                z = z*z + c

                if abs(z) > 2.0:

                    div = 1

                j = j + 1

        if (y > 1.0) or (y < -1.0) or (x > 1.0):  # apply more divergence criteria

            div = 1

        if div == 0:  # print complex values associated with non-divergent sequences
            print x,y

        y = y + dy

    x = x + dx