Potential Drop across capacitor

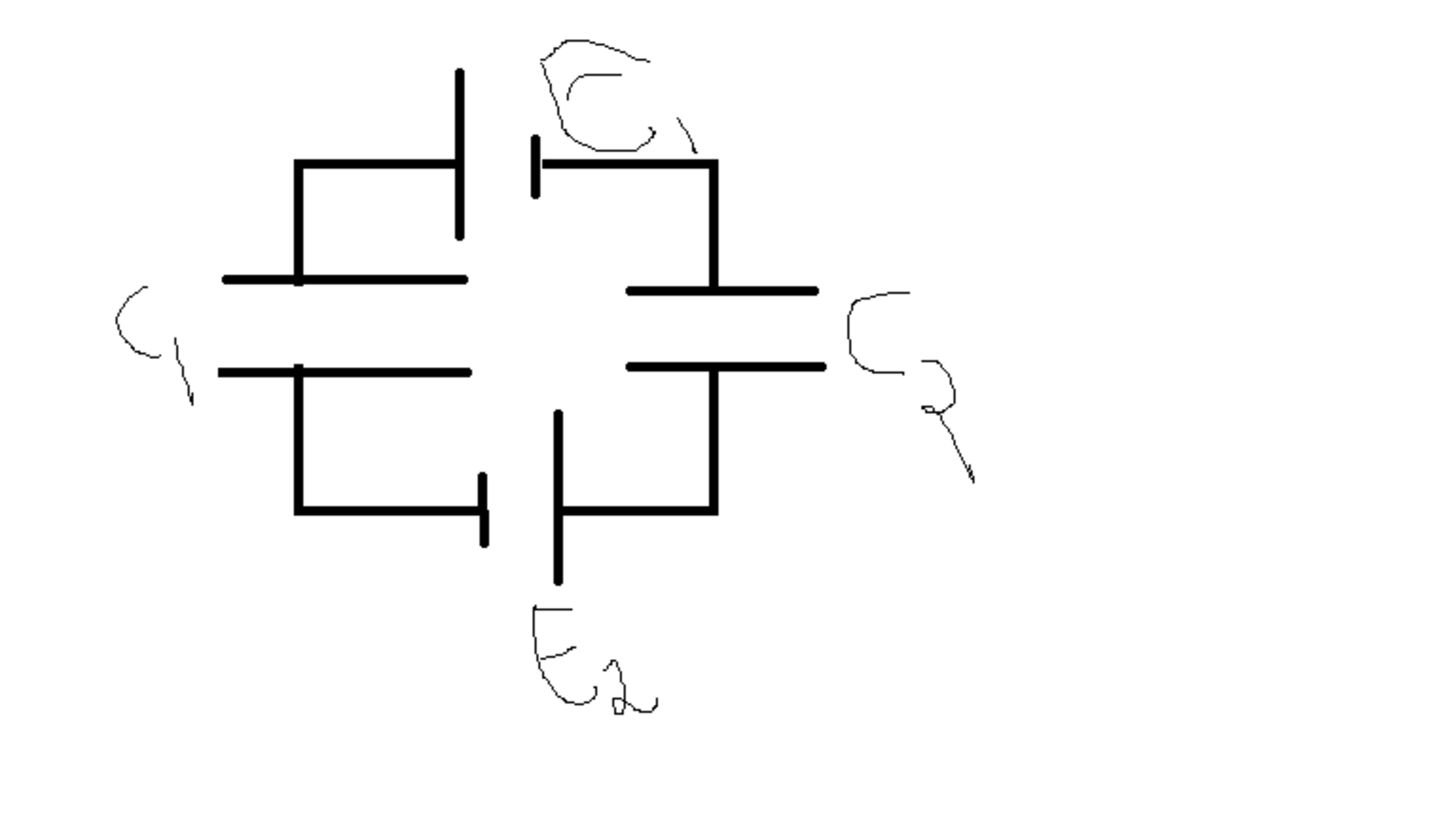
Find the potential drop across capacitor $C_1$

[hide=Try it!] Interesting Problem![/hide]

#Physics #ElectricityAndMagnetism #PhysicsProblem

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

$\frac{C_{2}(E_{1} +E_{2})}{C_{1} + C_{2}}$

jatin yadav - 7 years, 10 months ago

Swap the positions of E2 and C2. You now have a simple voltage divider.

Jimmy Kariznov - 7 years, 10 months ago

swapping them won't make a difference?

can you please explain a bit more?

hemang sarkar - 7 years, 10 months ago

nice writing :D

Rafael Muzzi - 7 years, 10 months ago

In steady state, charges stored in the capacitors must be same. Then, we just have to apply Kirchoff's Law.

Sambit Senapati - 7 years, 10 months ago

Not only at steady state , but at all time instants charges stored in capacitors would be same.

jatin yadav - 7 years, 10 months ago

yes, of course.

Sambit Senapati - 7 years, 10 months ago

how? can you explain a bit more?

Advitiya Brijesh - 7 years, 10 months ago

@Advitiya Brijesh – $q_{cap.} = \int\limits_0^ti_{cap.}(t) dt$ . Since , $i_{cap.}(t)$ is same for both capacitors ( as the circuit is complete ) , $q_{cap.}$ would also be same for both at any instant .I have assumed that initial charges of both capacitors is zero. (else the question would have been tidious and answer would have been a function of time.)

jatin yadav - 7 years, 10 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$