Principle of Inclusion and Exclusion

The Principle of Inclusion and Exclusion (PIE) is a way to calculate the number of elements that satisfy at least one of several given properties. If there are two sets, the principle of inclusion and exclusion states

$|A \cup B| = |A|+|B| - |A\cap B|.$

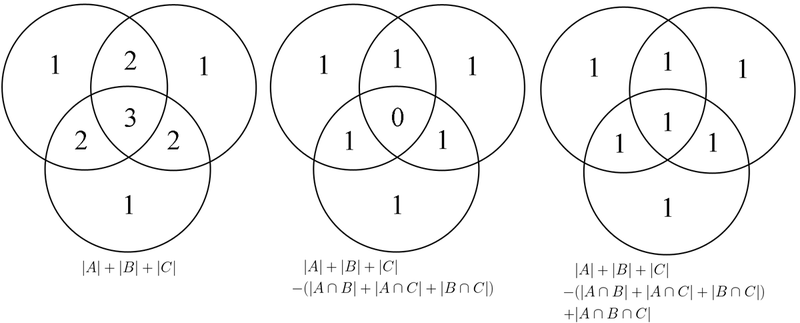
If there are three sets, the principle of inclusion and exclusion states
$|A\cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C|.$

We can verify these statements for ourselves by considering the Venn Diagram of events.

More generally, if $A_1, A_2, \ldots A_n$ are finite sets, then the principle of inclusion and exclusion states

$\displaystyle \left|\bigcup_{i=1}^n A_i\right| =\sum_{i=1}^n\left|A_i\right| -\sum_{1 \leq i < j \leq n}\left|A_i\cap A_j\right| +\sum_{1\leq i < j < k \leq n}\left|A_i\cap A_j\cap A_k\right| \\-\ \cdots\ + \left(-1\right)^{n-1} \left|A_1\cap\cdots\cap A_n\right|.$

Worked Examples

1. How many integers from 1 to 100 are multiples of 2 or 3?

Solution: Let $A$ be the set of integers from 1 to 100 that are multiples of 2 $( \lvert A \rvert = 50)$. Let $B$ be the set of integers from 1 to 100 that are multiples of 3 $( \lvert B \rvert = 33)$. Now, $A \cap B$ is the set of integers from 1 to 100 that are multiples of both 2 and 3, hence are multiples of 6 $( \vert A \cap B \rvert = 16 )$. By PIE, $| A\cup B| = |A|+|B|-|A\cap B| = 50 + 33 - 16 = 67.$

2. What is the sum of all integers from 1 to 100 that are multiples of 2 or 3?

Solution: While PIE is often used to count the elements of a set, if we remove the $| \cdot |$ symbols, the statement is still true. For example, in two variables, $A \cup B = A \cup B - A \cap B$. The same proof using Venn diagrams works to show that each element is included once. As such, the sum of elements in $A \cup B$ is equal to the sum of elements in $A$ plus the sum of elements in $B$ minus the sum of elements in $A\cap B$. Letting $A$ be the set of multiples of 2, and $B$ be the set of multiples of 3, then $A \cap B$ is the set of multiples of 6, hence the sum of $A \cup B$ is $\frac {(2+100)\times 50}{2} + \frac {(3 +99)\times 33}{2} - \frac {(6+96)\times 16}{2} = 3417.$

3. [Derangements] There are eight guests at a Secret Santa party. Each guest brings a gift and each receives another gift in return. No one is allowed to receive the gift they brought. How many ways are there to distribute the gifts?

Let $A$ denote the set of ways to distribute gifts such that everyone receives a gift, possibly their own. Let $A_i$ denote the set of ways to distribute gifts such that person $i$ receives his or her own gift. Then we would like to find

$|A| - |A_1 \cup A_2 \cup \ldots \cup A_8|.$

Since $A_i$ is the set of ways for person $i$ to receive his/her own gift, there are 7 choices of gifts for the next person, 6 choices of gifts for the following person, and so on. By the rule of product,

$|A_i|=7\times 6 \times \ldots \times 2 \times 1 = 7!$

Since $A_i \cap A_j$ is the set of ways person $i$ and person $j$ both receive their own gifts, there are 6 choices of gifts for the next person, 5 choices of gifts for the following person, and so on. Again by the rule of product,

$|A_i \cap A_j| = 6 \times 4 \times \ldots \times 2 \times 1| = 6!$

By continuing this argument, if $k$ people receive their own gifts, then there are $(8-k)!$ possible ways. Applying PIE, we obtain

$|A| - |A_1 \cup A_2 \cup \ldots \cup A_8| = 8! - {8 \choose 1} \times 7! + {8\choose 2} \times 6! - \ldots + {8 \choose 8} \times 1! = 14833.$

Note: A derangement of $n$ objects is a permutation of the objects such that none of them stay in the same place. The number of ways this can be done is denoted $D_n$, and this calculation shows $D_8 = 14833$.

4. We have 7 balls each of different colors (red, orange, yellow, green, blue, indigo, violet) and 3 boxes each of different shapes (tetrahedron, cube, dodecahedron). How many ways are there to place these 7 balls into the 3 boxes such that each box contains at least 1 ball?

Solution: Let $X$ be the total number of ways we can distribute the balls if there are no restriction. Each ball can be placed into any one of the 3 boxes, so $|X|=3^7$. Let $T$ be the set of ways such that the tetrahedron box has no balls, $C$ be the set of ways such that the cube box has no balls and $D$ be the set of ways such that the dodecahedron box has no balls. We would like to find

$|X| - |T \cup C \cup D|.$

We have $|T| = |C| = |D| = 2^7$, since the balls can be placed into one of the two other boxes, and $|T\cap C | = |C \cap D| = |D \cap T| = 1^7$, since all the balls must be placed in the remaining box, and $|T\cap C \cap D| = 0$. Hence, PIE implies

$|X| - |T \cup C \cup D| = 3^7 - 3 \times 2^7 + 3 \times 1^7 - 0 = 1806.$