Problem of two honest buddies
Hello Everyone,
Skip this para If you want to you dive into the problem. Some of you guys might be pushed (as I am going to mention you in comment after writing this) or you might be visiting this discussion on your own. In both circumstances my colossal thanks to you guys Because I was wondering about the solution of this problem and was getting different explanations from every part of internet most of them were wrong so now I might get the answer.
PROBLEM IS HERE :- Problem is as follows two plane mirrors are placed at an angle of 50 degrees to each other and an object(point sized) is placed symmetrically between them You has to find the no. of images formed.
- You use any formula provide it. I used a formula it gives answer which differs from my graphical solution. [I prefer you provide your solution with some graphical representation like an image I am providing below.]
Below are two images one is an example for an angle between mirrors 90 degrees other is for 50 degrees as asked in question.
- Better If open images in new tab.
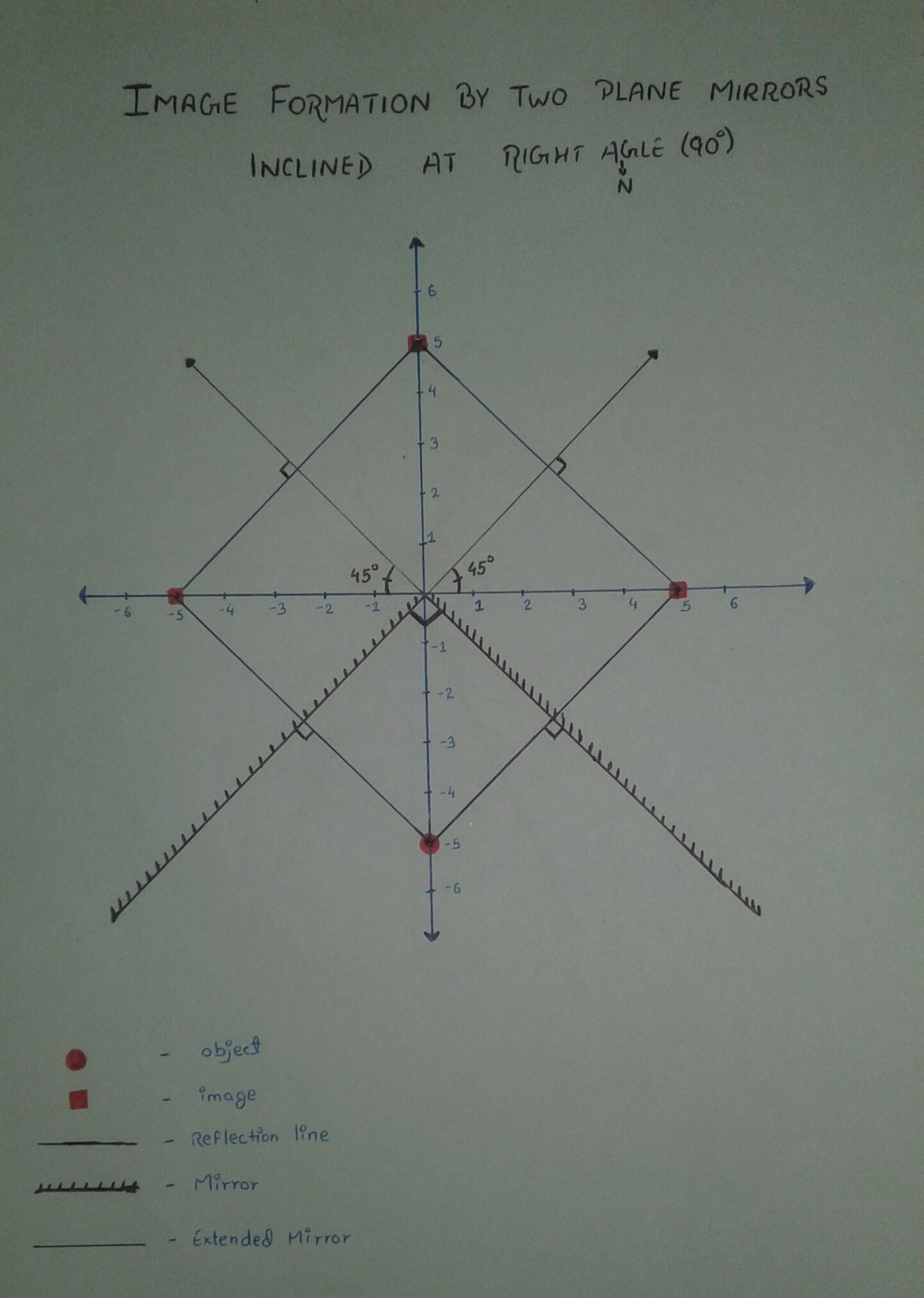
Edited : I find out some of you have problem in understanding the images so a short explanation here ==>
You can see mirrors in third and fourth quadrant and object is at -ve y axes at a distance of -5 from origin them first to images are formed by two mirrors Ɪ1 and Ɪ2 then what happens is image Ɪ2 works as a virtual object for left side mirror and Ɪ1 works as a virtual object for right side mirror and then It happens again and again. This stops when any images go beyond the mirror(extended) because then Image cannot work as virtual object. Below are given virtual object/object and their images.
O ---> Ɪ1 , Ɪ2
Ɪ1 ---> Ɪ3 , Ɪ2 ---> Ɪ4
Ɪ3 ---> Ɪ5 , Ɪ4 ---> Ɪ6
Ɪ5 ---> Ɪ7 , Ɪ6 ---> Ɪ8
Laws used in Graph-
- line joining image and object/virtual object is perpendicular to mirror.
Distance of image is equal to Distance of object from mirror/origin.
Thank you very much for visiting
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
This video is helpful for visualizing this problem and the equation n=θ°360°−1: https://www.youtube.com/watch?v=6maFbmPCnzY&feature=youtu.be
If the angle were 45°, the number of images would be 45°360°−1=7, and if the angle were 5171°, the number of images would be 5171°360°−1=6. In this problem, since the angle 50° is between 45° and 5171°, there should be 6 full images and 1 partial image of the object.
Log in to reply
Nice video link!
Nice.
Here is a diagram:
The left mirror L is reflected in the right mirror R to L', and the right mirror R is reflected in the left mirror L to R'. Then R is reflected in L' to R'', L is reflected in R' to L'', L is reflected in L' to L''', and R is reflected in R' to R'''.
The result is 6 full images and 1 partial image of the object.
Log in to reply
You took object wide. But if it is point sized two more images will be formed despite of one partial image. I think.
Log in to reply
A point-sized object can be inferred from the diagram. If the point is on the extreme left or right sides of the bar, then there are 7 images, but if the point is on the center of the bar, then there are only 6 images. So a point-sized object placed symmetrically between the two mirrors as described in the question would be like a point on the center of the bar, and would only have 6 images.
Log in to reply
Nice draw , BONUS : draw an arrow along object , to see what image is inverted or not
Log in to reply
To show inversion, I edited the picture so that one edge of the object is red.
Log in to reply
Brilliant then. :)
The difference between the video David posted and the situation here: the posted video has an object that extends from mirror to mirror, but this problem has a point object.
So when the video shows that 7.2 objects are visible, these are: (a) the original object; (b) six complete images; (c) two partial images of only 1/10th of the object.
Our point object corresponds to the center of the larger object shown in the video. If we look on straight, we can see only six images. But turning our head left or right, we can catch sight of two more.
In my opinion, 6 images.
My way to deal with these cases is always the same: reflect the world around the mirrors, and reflect again, and again. In the drawing below, left side, you have the direct visible world inside the mirrors, and that one reflected a first time. The green arrow shows where the right mirror puts its first image. The right side shows the full schematic... after repeated reflections over the real mirrors (green), or a single reflection (in this case) over the image of each mirror produced by the previous first reflection operation (yellow).
This way, you don't need to concern in doing ray reflections... from source to eye-sight, the light can be made to trace a straight line. By mirroring image over the mirrors, your straight line passing through a mirror is equivalent to one that reflects using reflection law. There is however a cardinal rule: The reflections over the right side mirror can only be picked through the right side mirror, and the same for the left mirror. If as an observer, you are in the middle, seeing the images of an object in the middle, by symmetrical mirrors α apart, you'll see only images at ±α, ±2α, ±3α, until ±180º. For instance, in that situation, you cannot see an image at X, because the light ray doesn't reach the eye through the right mirror (trace a ray and it doesn't cross it... things might be different with a different position for the observer, or if the mirror were semi-transparent and extended behind too).
From this, you can see the number of images seen is:
2⌊α180⌋
...when α does not divides 180º, and that number minus 1, when it divides. In our case:
2⌊50180⌋=2×3=6
PS.: I think I was too naive in my answer. When you asked how many images, I thought in images I can see... I'm not recalling well the definition of images in more formal contexts, nor will I try to recall it better, because I/you may have learn differently. But I thought I might be more precise in what I was meaning. First, I don't have any problem with what you did. You have a typo in an angle, it should be 100º where you have 110º, but beside that, I think I understand what you did and I have no qualms with that. Second, my 6 image guess is for an observer in the middle of the mirrors (A position). At that position, he'll see the original object and 6 images in the mirrors. But if he changes place, for the B position, he'll see 7 images.
Finally, C presents a scenario where we might be aware of 8 images at the same time.
An optical system changes the direction of light, in particular, the light emanated from sources of light we call objects. An image by an optical system is, for me, the point where we would have to put objects to get the same effect if we had not the optical system. This personal definition is probably my source of trouble with your problem, since it leads me to a different number of images depending on the position of an observer. If however we are talking about the full of positions where images can be, then I must agree with the number 8 of your and other answers. The way to prove it is by making a lens big enough to capture all the light between the mirrors, and project it in images after. Then, we'll discover there are 8 images.
By the way, I did the actual experiment with two mirrored doors in my bathroom, making 50º between them. The results agreed with what I said.
Log in to reply
What are you measuring a , 2a , 3a and 180 from. And if you can't see X then you have only for images in your diagram.
Please can you kindly see my image and tell me if i made images wrongly and if not why will i not able to see my last two images. It will help me understand.
Log in to reply
I added some additional information to original comment... just in case to edit it, does not notificate you.
If you move place of observer , image not move their position, I think you can see or not depending if real ray is intersepted . To prove that is necesary to draw this ray. Is diferent if object moves ( or object with more than one points) , in that case images move too.
@Mahdi Raza, @David Vreken, @Vinayak Srivastava, @Ram Mohith, @Hamza Anushath, @jordi curto, @Vikram Karki, @Stef Smith, @Alak Bhattacharya, @Páll Márton, @Maria Paszkiewicz, @Finnley Paolella, @Hana Wehbi, @Yajat Shamji, @Richard Desper, @Pi Han Goh
Log in to reply
I know only these people with great minds (excluding me)
Thought to give you some help!
Log in to reply
I have many exams, so I can't help you in this week.
Log in to reply
No problem, All the Best for Exams.
Log in to reply
Thanks!
Thank you very much. Much appreciated.
And you are too with a beautiful mind.
Log in to reply
Thanks a lot for the kind words @Vikram Karki!
You added me too and said with great mind. LOL
I want to say:
Log in to reply
Me too, but I tried learning it for the sake of this question
Yeah, but now you might be able to learn some concepts of reflection when there are two mirrors.
Before School. Exciting Huh?
Hello Vikram ,
The formula a think is Integer ( 360/50) -1 . That mean on produce 6 images.
I did'n prove that yet , but I will explain way I would do:
Graphicaly all posible ray starting at point has to retorn same point , First ray is that perpendicular at mirror right .Second ray 25º to normal mirror right and reflect to left mirror and for simetry retorn to point . Third ray is 50 º to normal right mirror reflect perpendicular to left mirror and retorn same path . This three ray has 3 more symetric on left mirror , total 6 rays returning to point , that implie 6 images , the ray going from point to vertice not retorn to point then not produice imagen .
PD: going on explanation : We can observe that over ski line (half right) ,angles that alow ray to retorn to point object are 25 , 50 and 75 next will be 100 but is greather than 90 and ray loose . Then number of good angles are Integer ( 90 / (50/2) ) and generalising with any angle between mirrors named "A" , number good angles right side = Integer(180/A) . By simetry , the same for left side ,we multiply by 2 , but if ray with 90º exist , we repeat that (case 180/A = integer) and we must sustract one repetition . Then formula will be : number of images (not including object) = 2 x (integer(180/A) - 1 x (180/A = integer)
Here is drawn only three images , by simmetry on can draw other three . Scale not correct :
Log in to reply
I read your PD.
You explained the image formation so, I added explanation of how i made my images and I was wondering if you can read and see if it is right [I think it is].
And I usually make images with paint these ones i just took via phone they automatically saved as png.
Log in to reply
Hello Vikram, while a interpret your draw , I will post mine in TODAY problem for same hours , and after will delete it . Try to see
Log in to reply
Ohh why there And how you made those three images i did not understand.
Log in to reply
I draw only three images for not to fill draw with a lot of lines , other three images are simmetryc of that . Is made with real ray . Distance between object and image no real ( not done with correct scale).
There are practical tools to draw that easily, but without real rays. (you can draw after).
You must considerer ( I supossed and done) , that point of view is located same place than object , that is normal when a person is the object , point of view can move and image keep at place but you must pay attention real rays are not intercepted and keep reflecting on real surface of mirrors.
Formula for angles is n x angle mirrors ( how you do in your draws from origen) , I used angles from object and over horizontal and is half of that . In your case n x angle must keek <= 180º , in mine <= 90º (but is same objective) . Your image Ɪ5 ---> Ɪ7 , Ɪ6 ---> Ɪ8 , violate that (angles greather than 180º for you) .
Your draw is OK for me , except I said images 7 and 8 . A litle lapsus 110º is 100º .
Try to draw over real rays.
Log in to reply
In my explanation Object/virtual object will be will form images until they are behind the mirrors - I used this. Ɪ5 and Ɪ6 are in front of mirror line so they will form images.
I will try to draw with real rays.
And 110 it was a typo :) I saw it after posting.
Thanks for your opinions. :)
Generally speaking, this can be done with any angle θ instead of 50∘. Thus it's formula will be θ360−1References: Quora answer, Video as mentioned by @David Vreken
Log in to reply
That means one original object, six images and one 20% of original object( exclude 80 % middle portion of original object).
Yes, @Mahdi Raza I know this formula and it contradicts with my graph this is why i posted this discussion.
I prefer you to observe my 2nd image or make one of your own to be sure.
[And Frankly speaking - this formula is kind of a trick doesn't always works.
And i don't believe quora I saw a explanation in that site in which a user was dividing 360/50 and his answer was 12.
And video mentioned by David Vreken has a good examples not explanation that formula is correct.]
Log in to reply
And I can prefer a video but it might be 1 and 1/2 hour long.
It is a video of youtube tutor who teaches according to cbse curriculum for JEE.
You might know him Physics Wallah-Alakh Pandey
Log in to reply
Yes I know him, though I don't watch his lectures on youtube very often
Log in to reply
His Videos are good.
I assume that the object is a point, infinitely small; so you cannot produce fractional images. The only situation in which you get an odd number of images is when the mirror image lies precisely on the line of symmetry. But that cannot be the case here.
It can be shown (I'm sure the video does this, too) that the image points and object lie on a circle, at an arc distance of 50˚ from each other. Thus, if we call the object's position 0˚, and the mirrors cross the circle in ±25˚, then the eight images will be located at ±50˚, ±100˚, ±150˚, ±200˚ (= ±160˚). These last two images will not be reflected further, because they lie on the wrong side of the planes of the mirrors.
In general, if the mirrors form angle α, the mirror images will be located at ±α,±2α,±3α,… up to, and including the first value ±nα where nα≥180˚. This suggests that the number of images is 2×⌈α180∘⌉, which is equal to 360∘/α rounded up to the next even integer. In case α∣180∘, the last image will lie precisely on the line of symmetry and we get an odd number of images, namely 360∘/α+1.
In this case, we get 360∘/50∘=7.2 which we round up to the next even integer, that is, 8.
Log in to reply
So , answer is 8
Log in to reply
Yes. As I said, it has to be even because of the obvious symmetry.
Log in to reply
NO, At that time I was talking about general case that it can be both odd or even for ex for 90 it is 3.
I think last two images ( red points in draw ) , don't exist . It will be there if would exist , but dosn't . Try to draw real ray to produce that.
Log in to reply
He has drawn the ray two small lines joining red points and preceding images.
Can you reason why they don't exist I really want to know.
Log in to reply
Imagen realy exist (virtual in this case) if you can draw real ray from object returning to object after necesary reflection . First 6 images do that , but last two not . Try to do it ( I mean real ray)
Log in to reply
I don't know if i got you right but I am going to make ray diagram for one of the red point images and post here.
Log in to reply
I tryed to post my draw , but at the moment I didn't get ,neither .
Now i don't know how to post a image in comment.
Log in to reply
I tryed too and diden't get .
Try creating a note, post a picture, and copy that text and paste it here. That should do the trick!
The last two can be done too:
Log in to reply
This ray don't retorn to original objet . This image can't be seen from object position. How you post draw?
Log in to reply
Upload in a note, and copy the link(not the URL :D). You don't have to submit the note.
Rays don't have to go to the original object. The ray must go to the eye of the observer.
Log in to reply
what if observer is at object's place.
What is this diagram about?
Log in to reply
It shows a light ray that shows in one of the images made by four reflections.
So, I am right about the solution and formula lies.
Or we have to know more on how to use this formula [360/angle-1]
Log in to reply
Note that he used the ceiling function (upper brackets) which means round up to nearest integer
Edit:
Indeed, it is not clear how to use this formula since there are various(right and wrong) explanations
Log in to reply
Yes, but I was talking about the formula everybody else is talking about in their solutions.
Do you mean even number of images (with repetitions)? There would be an odd number of distinct images if the last two happen to overlap
Based on the formula 2×⌈α180⌉
I shall write it as :
2×⌈α180⌉+⌈α180⌉−⌊α180⌋−1
Where :
The additional part will be (-1 if α is a factor of 180) and (0 otherwise)
This will include both cases. However, it is a bit complicated to write.
Okay sir Can you explain the part from the formula you provided. I didn't get it.
Shouldn't the mirrors themselves also be reflected in each other?
Log in to reply
This is what happening when we took a image and consider it a virtual object for other mirror and make another image.
I had added explanation in the note later.
Log in to reply
With your picture, Vikram, I'm having trouble with you using the extended part of the mirror to reflect the points (for example, I3 to I5, I5 to I7, I4 to I6, I6 to I8), because that extended part of the mirror is behind the original mirrors. I think the multiple images have to come from the multiple reflections of the original mirrors in each other.
Log in to reply
Okay, I understand that it might difficult.
We can reflect images using extended mirrors it is valid i have checked it obeys all laws.
why i did that because using real mirror for all formations will turn out to be messy more than it is now.
And difficult too for last two images because they are real close to mirrors. ray diagram will be too messy.
It think the answer is that eight images are formed.
I am not sure, and I don't know whether I am right or not
I don't know these type of questions
-EDIT-
I GOT THE ANSWER
The formula I used is x°360° (if and only x°360° is odd, if it is even, we use x°360°−1 )
50°360°=7.2
As seven is odd, and it is approximately near to the answer we got, 7.2, we need not subtract, and there are in total approximately seven images formed.
It might be safe to say that seven images are formed
Log in to reply
yup my answer is same.
But to be sure and confident i posted so that people with great minds(as you said) can help.
Log in to reply
@Vikram Karki, I gave the answer now; hope you can understand!
Log in to reply
@Vikram Karki, I will post a graphical solution soon...
Stay tuned!
x is 50
Log in to reply
Hahaha, thanks for mentioning! Didn't read the main question properly!
I know about this formula and it contradicts with my graphical illustration.
actually this is the formula which started all this havoc(kind of) for the solution of this problem.
Log in to reply
I will try to put on a graphical illustration...
That may help
I think this one is based on this principle
Multiple reflections is equivalent to"reflecting" the real world multiple times. Imagine dividing a circle into portions of 50° each. There would be 7 complete reflections.
Your method is a different. You reflect the same point along the mirror lines as axis of reflections. Thus, you got 8.
I don't know which one is correct. You would reach the same conclusion either way if you use factors of 180° such as 30° . Try angles like 40° first using both methods.
Log in to reply
I do agree dividing circle in portions of given angle works sometimes for eg. for the angles 90,30,even 40. But only
-when object is symmetric to both mirrors
-And for Large angles like 90 and small angles like 30.
Its is kind of a trick and tricks don't always work.
I worked on the angle of 40 the trick worked but just barely what if you increased angle to 45 it works both ways.
But it is not working for 50
Actually one of them is the original object, so maybe 6 is the answer
I only understand the first pair of images, don't know how you progress after that.
Log in to reply
Actually I did the same as first.
Look carefully.
And please ask what you didn't get.
I would argue that the number of images should be even, because of symmetry.
Log in to reply
Not sure, but that depends on the angle between the two plane mirrors
Not truly,
Sometimes no. of images comes to be odd as half of image is produced by one mirror and half of image is produced by other.
Sometimes two images overlap causing decrease in one image.
What i want you to do is observe my 2nd image it is the image formation on a cartesian plane. I had used simple reflection laws to form that and no. of images comes out to be 8.
[I have added explanation in the note.]
Your picture is incorrect. The second image should be 100∘
Log in to reply
who are you saying to?
Because 90+10=100 and 90+10 can't be 110.
But Vikram's drawing has 90 + 10 = 100˚, as it should be.
Log in to reply
Yes, but he wrote that incorrectly.
Log in to reply
You're quite a observer.
I never noticed that. God gifted you with a sharp eye @Páll Márton
Log in to reply
I thought no one will notice that
Oh yes, talking about the small image in corner of 2nd.
In my Physics Online Class of this year, I was told the same formula given by @David Vreken and @Mahdi Raza, but it is also told that the no. of images is always odd, I don't know why.
Log in to reply
Not always, Sometimes two images overlap but formula counts both images and we have to remove that ourselves. for ex: if angle is 90 degrees 360/90 = 4 (even) ==> subtract 1 = 3 in this case last two images overlap(you can see image in my post above).
In my school we are not taught how to use this formula properly this is why I don't always use it.(I sometimes do)
A similar problem