Problem Writing Party: July 11th - July 24th - Calvin Lin

Problem Writing Party 10 had a ton of discussion, and lots of people were contributing various problems to it. You may have noticed that we started adding some new chapters like Operator Search, Syllogistic Logic, Composite Figures and Convergence of Sequences, indicating that we're expanding the availability of material on Brilliant. Unfortunately, this introduced confusion, as it wasn't immediately clear what was / was not allowed into the chapter. As such, we will only be adding existing chapters to the PWP, so that everyone can easily reference the relevant material.

Once again, I'm working on creating the quizzes, and will update the following list ASAP. The new chapters will take a bit more time for us to create, and I am hoping for them to be released at the end of the week.

Some of you would also have received B-notifications that your problems were added to the quizzes over the course of the previous week. Keep it up! We value your submissions, and would love to feature more of them.

Here are the quizzes that the Brilliant community helped create:

New Brilliant Challenge Quizzes

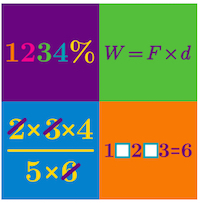
Properties of Arithmetic: Level 1, Level 2
Operator Search: Level 2, Level 3, Level 4
Percentages: Level 1, Level 2
Syllogistic Logic
Composite Figures: Level 2, Level 3, Level 4
Convergence of Sequences
Work: Level 2, Level 3
$\quad$

Let's kick off our 10th Problem Writing Party!

How it Works

The party starts right now (July 12th, 2016) and will last for the next two weeks. We will be focusing on writing awesome problems for the topics listed in quizzes that need your help on the publish page.

We will be picking the best few problems for each topic and they will be immortalized and formed into a challenge quiz.

Do participate in attaining a sense of accomplishment and a growth in problem writing skills!

The topics are:

Topic	Descriptions	Great Problems
Absolute value	$\|x\|$ is the distance from from 0 to $x$ on the number line. How do we interpret $\|x-y\|$ ?	Level 2, 3
Linear Inequalities	We know that $1 < 2$ , but is it also true that $x<2x$ ?	Level 1, 2, 3
Radical Expressions	Is it true that $\sqrt a \times \sqrt b = \sqrt{ab}$ ?	Level 1, 2, 3
Uniform Circular Motion	Uniform circular motion describes objects that move along a curve of a constant radius at constant speed.	Level 1, 2, 3
Variance	I have two distributions. Which distributions is more sparse than the other?	Level 2, 3
Discrete Random Variables	Would you rather flip 10 fair coins or 10 biased coins in hopes of getting 5 heads and 5 tails?	Level 2, 3, 4
Heaps	Heaps are data structures which are maintained in a way so that finding the minimum or the maximum is always efficient.	Level 1, 2

Use this note to

Ask questions about the party or brainstorming ideas from Brilliant staff.
Share links to great relevant problems.
Bounce your ideas off each other to help formulate the best problem you can.
If you're posting your problems, please keep it to one rooted comment (and I will be merging such comments from the same person). This helps us keep the page more orderly.
You can link to your own problems by using the markdown syntax of [text](url link).

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Here is a collection of my coin flipping problems that could likely be added to the discrete variable problems:

Enjoy! Geoff

Geoff Pilling - 4 years, 11 months ago

These are simple and nice questions. I'm still wondering how you solve the 5 equations simultaneously in Flipping A Binary Coin.

Pi Han Goh - 4 years, 11 months ago

I used an online linear equations solver! :)

@Geoff Pilling – DO share with us! What app is that?

@Pi Han Goh – This is my favorite one

Enjoy! :)

@Geoff Pilling – Or you can Google "Linear Equation System Calculator". I found another one that can enter 4×4 all the way to 12×12

Hung Woei Neoh - 4 years, 11 months ago

@Hung Woei Neoh – SHARE SHARE! =D

@Pi Han Goh – Lol!

Ashish Menon - 4 years, 11 months ago

@Ashish Menon – Sorry, I remembered wrongly. It's 2X2 to 11X11

Check it out!

It shows results in decimals and fractions both. I used this to write this solution

@Geoff Pilling – Wow, the link you gave is good!

Hobart Pao - 4 years, 11 months ago

I think most of your radical questions are super duper hard because we need to deal with convergence, which is another hard issue to tackle.

Here is my submission -Minimum Value

Anuj Shikarkhane - 4 years, 11 months ago

Ahh this one is nice!! @Rishabh Cool's solution was unexpected. I thought the only way to solve this is via case by case analysis. Reshared!

Thanks!

I have several radical expressions problems here which I would like to be considered for this Problem Writing Party. Here they are!

Enjoy! I apologize that these were posted late, and I really hope that you guys will forgive me. :)

Jonas Katona - 4 years, 10 months ago

"How about 4, 5, 6?" looks like a number theory question. Reshared

Nevertheless, you got very nice set of questions as usual.

Pi Han Goh - 4 years, 10 months ago

Thank you so much, Pi Han! You always take the time to try solving all of my problems, it seems. I really appreciate that. :)

Btw, for the "Putting it through twice" problem, I looked back and finally understood your frustration; that's why I changed the problem to how you wanted it. I apologize for the trouble; I sometimes make careless mistakes because I forget to look at how everything fits together. I am glad that you take the time to look at things thoroughly, because you would find faults which very few others would notice (as with this one).

@Jonas Katona – Don't worry about it. We're all helping each other here! =D

This is my entry for Absolute number: Zero Sum Game.

My new one on Inequalities: Think Positive.

Here's mine on Discrete variables: Hit the Jackpot.

Worranat Pakornrat - 4 years, 11 months ago

Nice twist on these topics.

For the absolute value question, my concern is that the origin lies in all 4 quadrants, and so we must be careful to explain how to deal with these cases. Perhaps, we could divide the expression by $xy$ ?

(Note: I've combined your comments)

Calvin Lin Staff - 4 years, 11 months ago

Thanks for the feedback. Yes, maybe I'll add that x,y are not zeros.

Worranat Pakornrat - 4 years, 10 months ago

For discrete random variables, I have this one

This is a really cool problem. I bet many of your other problems regarding coin flippings also fit into this category.

Agnishom Chattopadhyay - 4 years, 11 months ago

Hey thanks, @Agnishom Chattopadhyay ! :-) When I get a chance I'll compile a list of links to my other coin flippers!

Good setup. The solution should briefly explain how one could arrive at the count. The usage of Markov chains to express the change of states could be a helpful framework.

Absolute Value Absolute Value 2

Linear Inequalities Linear Inequalities 2

Variance

Chung Kevin - 4 years, 11 months ago

Nice set of questions. This got me thinking: What is the shape of the graph $|x_1 | + |x_2| + |x_3| + \cdots + |x_n| = 1$ ?

Heaps: This is really an addition problem, Towards better heaps, d-ary heaps
Absolute Values: Colorful Absolutes
Variance: Erratic Systematic Wormhole Variance

The plot is not showing properly

Thanks. Fixed.

For your first question, I was wondering how you get the number $1.374 \times 10 ^{284}$ . Interesting setup, now I have to go and read the Heaps wiki.

Still, I have no idea what your last question is talking about, though. Reshared anyway!!

Here is my first submission for variance.
Here is my second submission for unoform circular motion.
Here is my third submission for circular motion.
Here is my fourth submission for radical expressions.
Here is my fifth submission for radical expressions.
Here is my sixth submission for radical expressions.
Here is my seventh submission for radical expressions.
Here is my eight submission for radical expressions.
Here is my ninth submission for radical expressions.
Here is my tenth submission for radical expressions.

Wow! You really have a cool collection of radical problems

Thanks! :)

Ah, the Fun with Exponents set. Brings back memories

Do you want more of those?

@Ashish Menon – Only if you have free time. Let me know when there's a new question. I'll check for typos again XD

@Hung Woei Neoh – Same. I used to look forward to those.

Sal Gard - 4 years, 11 months ago

Absolute value and complex number is my question about absolute value .

Tommy Li - 4 years, 11 months ago

I was wondering: How did you find the square root of that large number in your penultimate step so easily?

I used calculator to do some calculation . No trick is involved .

Uniform Circular Motion: "Around and around"

Michael Fuller - 4 years, 11 months ago

Here are my problems, list will be expanded as more are added.

Uniform Circular Motion

Absolute Value

Radicals

Radical radicals (aka. "Some brute force & luck needed: Part II")

Wee Xian Bin - 4 years, 11 months ago

Ahh! I love your second last question. It feels like a mixture of inequalities of polynomials and absolute value properties. I'm still struggling with your last question though...

@Pi Han Goh You may want to try my older radical problem and my Some Brute Force & Luck Needed Part 1 problems first for a feel then :)

Absolute value - Not sure if this qualifies

In my humble opinion, it does. I also think it is a good problem

Hmmm, this feels like an amalgamation of absolute values and floor/ceiling functions which require us to know various backgrounds before solving it first. To be honest, this seems more like a ceiling/floor question.

Becuase floor/ceiling functions tend to be studied later than absolute values, I'm also inclined to place this under floor/ceiling. This is a great quesiton though :)

Here are some dice rolling ones which could likely be considered as discrete random variables:

Here is a computer science problem I created. I think this should be placed in level 5 but I was unable to do that because of my own level. @Calvin Lin : Can you kindly do this? Thanks

Snehal Shekatkar - 4 years, 11 months ago

I think this problem would be better suited to Level 4. I have changed the level of the problem.

The convert number to number name problem seems interesting. However, I think counting up the number of straightlines in each letter makes it a little tedious.

@Agnishom Chattopadhyay: I don't understand. Why? There are only 26 letters.

@Snehal Shekatkar – Alright then :). How many letters would you find tedious yourself?

Hmmm, this does not look like a heaps question. Am I mistaken?

@Pi Han Goh : I'm sorry. Didn't get you.

@Snehal Shekatkar – Sorry. Autocorrect. Fixed.

My contribution for Absolut Value

Hjalmar Orellana Soto - 4 years, 11 months ago

Ah! This is cute. I love how the positions of the absolute value signs change everything!

Indeed, that was a fun question to work on :)

One for Radical Expresions

Here's mine on Discrete Variables: Infinity Game, Grab & Guess.

And for Radical Expressions: Radical Sums.

Nice questions, providing a scenario where the distribution occurs makes it more enticing for people to think about.

Thanks. I was busy with my new work lately. I'll try to come up with new ones soon. ;)

Here's my submission for radical expressions.

Louie Dy - 4 years, 11 months ago

Hmmm, I think you're missing a lot of steps in your solution. How did you prove that it converges?

As pointed out, care has to be taken when dealing with infinite sequences. Sometimes, they could tend to infinity, and still satisfy the equation $x = 2x$ , which doesn't imply that $x = 0$ .

This is my new question on Variance: Sunny Shoot-out.

Nice problem! How did you manage to generate the graphics?

Thanks. I drew it myself. Still far from Van Gogh's Sun flowers. Lol...

The set up of the problem makes it interesting! I liked it :)

Pranshu Gaba - 4 years, 11 months ago

I really liked it too :)

@Calvin Lin – Thanks. Took me a while to draw the flowers though. LOL...

Thanks. I was about to draw children at first, but my graphic skills are not that great.

Here are my second round of entries

Absolute value 3, Absolute value 4, Absolute value 5.
Linear inequalities 4, Linear inequalities 5.
Radical expressions 2, Radical expressions 3, Radical expressions 4.
Variance 4, Variance 5.
Discrete Random Variables 1, Discrete Random Variables 2.

Here my number theory problem.

Hmmmm. I'm curious. Which topic does this question fit inside?

I am not sure. May be you can guide me :)

@Snehal Shekatkar – Calvin wished to have problems in Absolute value, Linear inequalities, Radical expressions, etc (in the table above) only. Your number theory question is nice but I don't think that is what he is looking for right now.

As a fairly new member, I am happy to submit Radical Mad. If someone could latex it, it would be appreciated. Thanks and @Calvin Lin sorry for previous inactivity in problem writing parties.

Sal Gard - 4 years, 10 months ago

Hmmm, this looks like multiple tedious algebraic manipulation questions merged into one. Have you tried simplifying your question? Because from the looks of it, it's just plain bashing.

Here are my entries::::

Absolute value 1, Absolute value 2

Radical Expressions 1

Linear Inequalities 1, Linear Inequalities 2, Linear Inequalities 3

Variance 1, Variance 2, Variance 3.

I like absolute value 2. I thought it was a nice setup, and am slightly sad that it has no solutions.

For variance 2, you have to be careful to make it such that the rv only takes on those values. Otherwise, we could have (say) $P(Y = 1000) = 0.1$ , which would affect the variance.

Oh right. Thanks for pointing it out. I've fixed it! =D

Here are my third round of entries

Absolute value 6.
Linear inequality 6.
Radical expressions 6.
Discrete Random Variables 3.

How can I join in Slack..??? @Calvin Lin

Sudhir Aripirala - 4 years, 10 months ago

https://brilliant.org/discussions/thread/rolle-theorem/

Rishabh Deep Singh - 4 years, 10 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$