Proof for area of any Regular Polygon 2!

Here is the link to my previous proof for the area of any quadrilateral being $\frac{ap}{2}$ where a is the apothem and p is the perimeter. These two notes are quite closely related and the other note helps you to get a better understanding of this note but it is not at all necessary.

In this note, I will prove that the area of any polygon is $\dfrac{1}{4} na^2\cot(\dfrac{\pi}{n})$ where n is the number of sides and a is the side length.

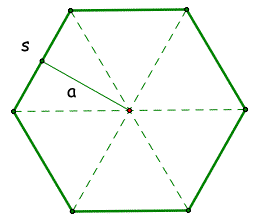
We start by drawing lines to each of the vertices of the polygon. Each of the angles will be congruent and of course add up to 360 deg. Thus since there are n angles (n being the number of sides), each angle is $\frac{360}{n}$ .

Next, we draw the perpendicular bisectors of each side. Because each of the interior triangles is isosceles, the bisector will bisect both the angle and the side length. This makes the base of each "half" triangle $\frac{a}{2}$ and the angle closest to the polygon's in-center $\frac{180}{n}\Rightarrow \frac{\pi}{n}$ ).

Next, we find the height of the triangle (which is equivalent to the apothem. In this case, because we are given the angle closest to the incenter of the polygon and the corresponding opposite side length $(\frac{a}{2})$ , we must multiply the base by $\cot\dfrac{\pi}{n}$ . By doing this, we are left with the height since cot represents (in this case) the $\frac{adjacent}{base}$ .

Then, we get the area of each triangle $\dfrac{b\times h}{2}\Rightarrow \dfrac{a\times (\dfrac{a}{2} \times (\cot\dfrac{\pi}{n}))}{2}\Rightarrow \dfrac{1}{4} a^2\cot(\dfrac{\pi}{n})$ .

Finally, because there are as many triangles as there are sides, we multiply our formula by n (the number of sides and are left with $\boxed{\dfrac{1}{4} na^2\cot(\dfrac{\pi}{n})}$ .

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Proof for area of any Regular Polygon 2!

Comments