Proof for the focus of a parabola/parebola :3

In this note I'll prove that the distance of the focus from the vertex $(p)$ of a parabola has the equation $4p(y-k)=(x-h)^2$ where the parabola has the vertex (h,k).

I would also love feed back on this note. If you look at most of my other notes, I go very far into detail about each step I do to avoid any confusion and to make the note understandable to as many people as possible. However, for the more skilled reader, it may seem a bit long, so this note I'll skip a few simple explanations (no details will be skipped). Tell me what you think in the comments below :) thanks!

Begin with the standard equation of a parabola $y=ax^2+bx+c$.

Finding the vertex coordinates using $x=\frac{-b}{2a}$

$y=\left(\frac{b^2}{4a}\right)-\frac{b^2}{2a}+c$

$y=\dfrac{-b^2}{4a}+c$

Our vertex has coordinates

$\left(\dfrac{-b}{2a},\dfrac{-b^2}{4a}+c\right)$

Thus $h=\dfrac{-b}{2a}$ and $k=\dfrac{-b^2}{4a}+c$

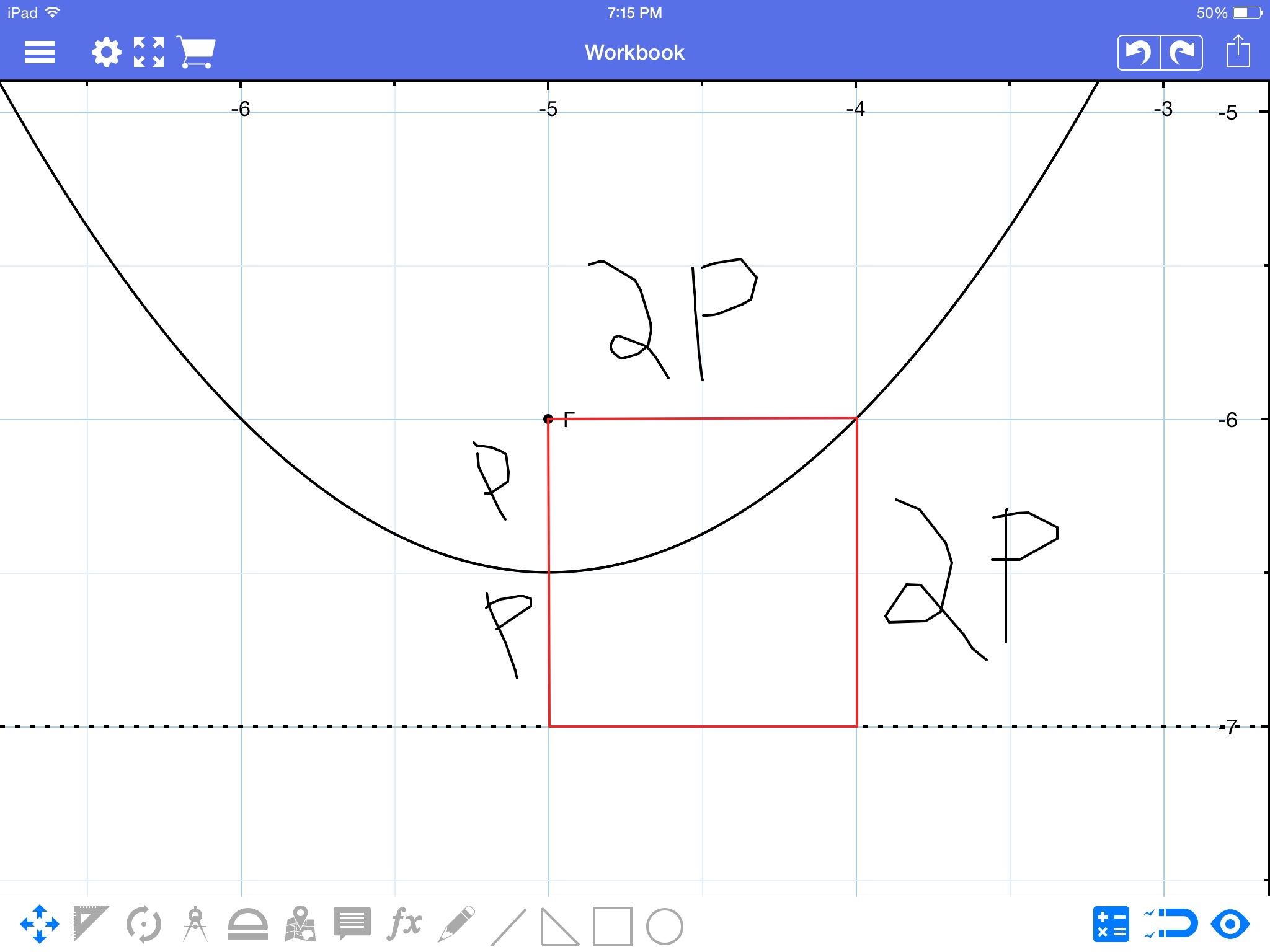
A parabola is the set of points equidistant from the focus and directrix. Thus there is a point (call it m) distance 2p from the focus and distance 2p from the directrix. Therefore, if we draw a line parallel to the directrix from the focus, it will perpendicularly bisect the line from the directrix to m. (Can someone explain why, I can't explain this for some reason, I know why, but I can't put it into words). This is what is depicted in the picture above.

Now, this means there exists a point on our graph distance 2p to the right of our vertex and distance p above. Thus the point has the coordinates $\left(\dfrac{-b}{2a}+2p,\dfrac{-b^2}{4a}+c+p\right)$. Plugging in for x and y

$\left(\dfrac{-b^2}{4a}+c+p\right)=a\left(\dfrac{-b}{2a}+2p\right)^2+b\left(\dfrac{-b}{2a}+2p\right)+c$

Bash bash bash

$\dfrac{1}{a}=4p$

Going back to our first equation $\left(\frac{1}{a}\right)y=x^2+\left(\frac{1}{a}\right)bx+\left(\frac{1}{a}\right)c$

$4py-4pc=x^2+4pbx$

This part is a little tricky so I'll show all the steps. Add $4p^2b^2$ to both sides.

$4p(y-c+b^2p)=x^2+4pbx+4p^2b^2$

Resubstituting $p=\dfrac{1}{4a}$ EVERYWHERE BUT THE FIRST P.

$4p\left(y-c+\frac{b^2}{4a}\right)=x^2+4pbx+\frac{4b^2}{16a^2}$

$4p\left(y-\left(\frac{-b^2}{4a}+c\right)\right)=\left(x-\left(\frac{-b}{2a}\right)\right)^2$

Remember, $h=\dfrac{-b}{2a}$ and $k=\dfrac{-b^2}{4a}+c$

$4p(y-k)=(x-h)^2$

And we are done.

Remember, please leave feed back on how you liked/disliked the writing style/comprehensiveness of this note.