Prove it

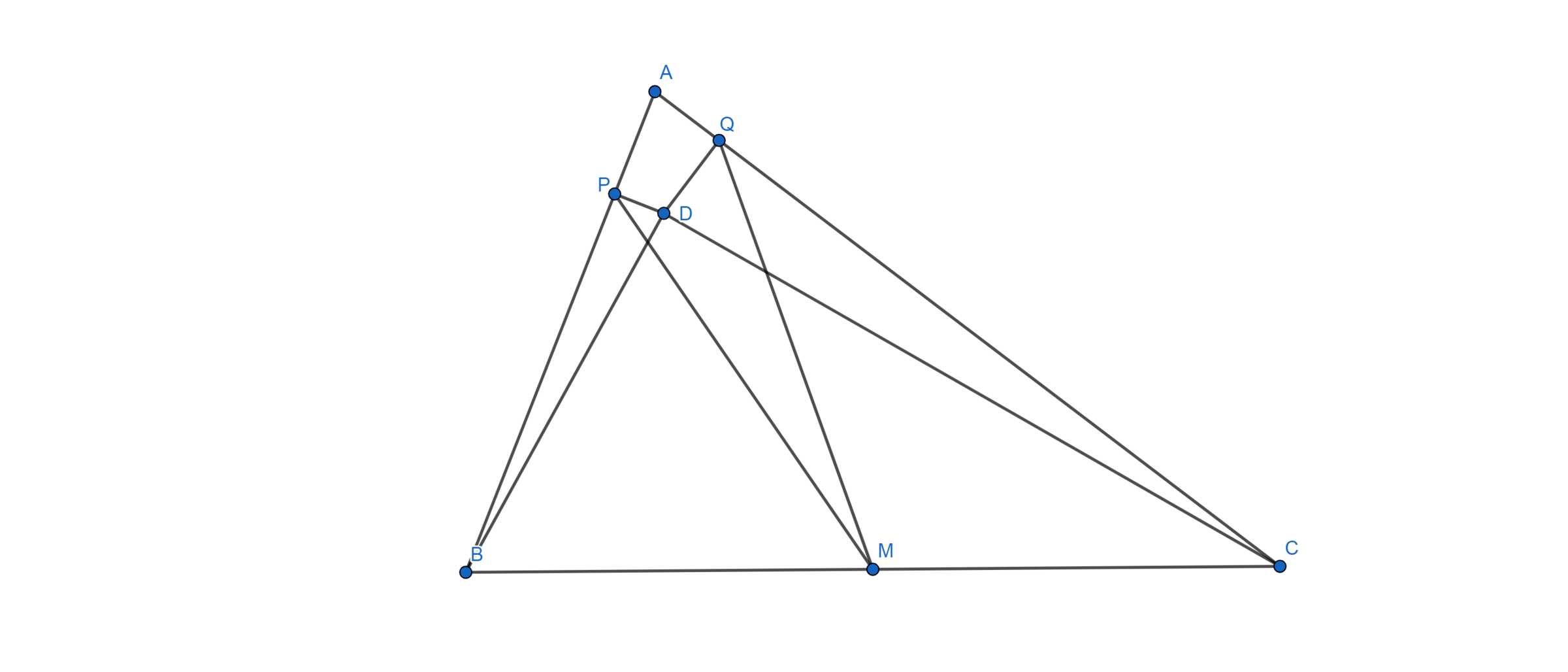
Suppose that P and Q are points on the sides AB and AC respectively of △ABC. The perpendiculars to the sides AB and AC at P and Q respectively meet at D, an interior point of △ABC. If M is the midpoint of BC, prove that PM = QM if and only if ∠BDP=∠CDQ .

I tried to come up with a solution using Euclidean geometry only, but to no avail.

#Geometry

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

$PM=QM$ is a direct result of the Nine-Point Circle Theorem

Sathvik Acharya - 5 months, 3 weeks ago

But P and Q are given to be random points on AB & AC respectively. And yes, the result holds when D is the orthocentre.

Abu Nazam Sk Md Tamimuddin - 5 months, 3 weeks ago

Sathvik Acharya - 5 months, 3 weeks ago

@Sathvik Acharya – But points P and Q are given to be random which indicates that points P, D and C should not be collinear necessarily. Same thing applies for points Q, D and B.

Abu Nazam Sk Md Tamimuddin - 5 months, 3 weeks ago

@Abu Nazam Sk Md Tamimuddin – Yes, but when the angles are equal, doesn't it imply that they are collinear (vertically opposite angles) ?

Sathvik Acharya - 5 months, 3 weeks ago

@Sathvik Acharya – No, not necessarily. It's still possible for them to be equal without being intersected in lines.

Abu Nazam Sk Md Tamimuddin - 5 months, 3 weeks ago

I found a solution here. https://math.stackexchange.com/questions/3961588/geometric-problem-concerning-relation-of-equal-segments-and-angles

Abu Nazam Sk Md Tamimuddin - 5 months, 2 weeks ago

That was a nice problem!

Sathvik Acharya - 5 months, 2 weeks ago

Indeed!

Abu Nazam Sk Md Tamimuddin - 5 months, 2 weeks ago

test

Banashri Banaja Laxmi Mohanty - 5 months, 3 weeks ago

I tested the result through a software. It holds.

Abu Nazam Sk Md Tamimuddin - 5 months, 3 weeks ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$