Question from IMO

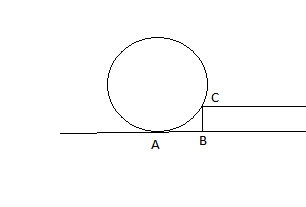
A hoop is resting vertically at stair case as shown in the diagram.AB=12cm and BC=8cm. The radius of the hoop is..

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

If you make a center point, let's call it O, then you know that OA=OC (both radii). If you extend the line of the stair (the one parallel to the ground) out horizontally, it will eventually intersect OA. Label this point of intersection D. Now you have formed a right triangle (triangle ODC). You know that BC=AD=8. Therefore OD=OA-AD=OA-8. You also know that AB=DC=12. Using the Pythagorean theorem, you can determine the length of OC. (OA-8)^{2}+12^{2}=OC^{2}. OA^{2}-18OA+64+144 =OC^{2}. OA^{2]-18OA+208=OC^{2}. Since OC=OA (both radii), we can plug in OA for OC. OA^{2}-18OA+208=OA^{2}. Then it is merely algebra. -18OA+208=0. 18OA=208. OA=208/18. OA=104/9.

Michael Thew - 7 years, 8 months ago

You have everything up to the Pythagorean theorem right. You messed up here: $(OA-8)^{2}+12^{2}=OC^{2}$ $OA^{2}-18OA+64+144 =OC^{2}$

The $-18OA$ should be $-16OA$ . This gives the correct answer $OA=13$ .

Daniel Chiu - 7 years, 8 months ago

Thank you for the correct answer!

neha adepu - 7 years, 8 months ago

Thanks a lot! It was of great help!

neha adepu - 7 years, 8 months ago

O thanks Daniel. I was wondering why it was such a messy fraction.

Michael Thew - 7 years, 8 months ago

Fuck offffff

Vinit Kumar - 4 years, 4 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$