Questions 2
1) Two pendulums of same amplitude but time period and start oscillating simultaneously from two opposite extreme positions. After how much time they will be in phase?
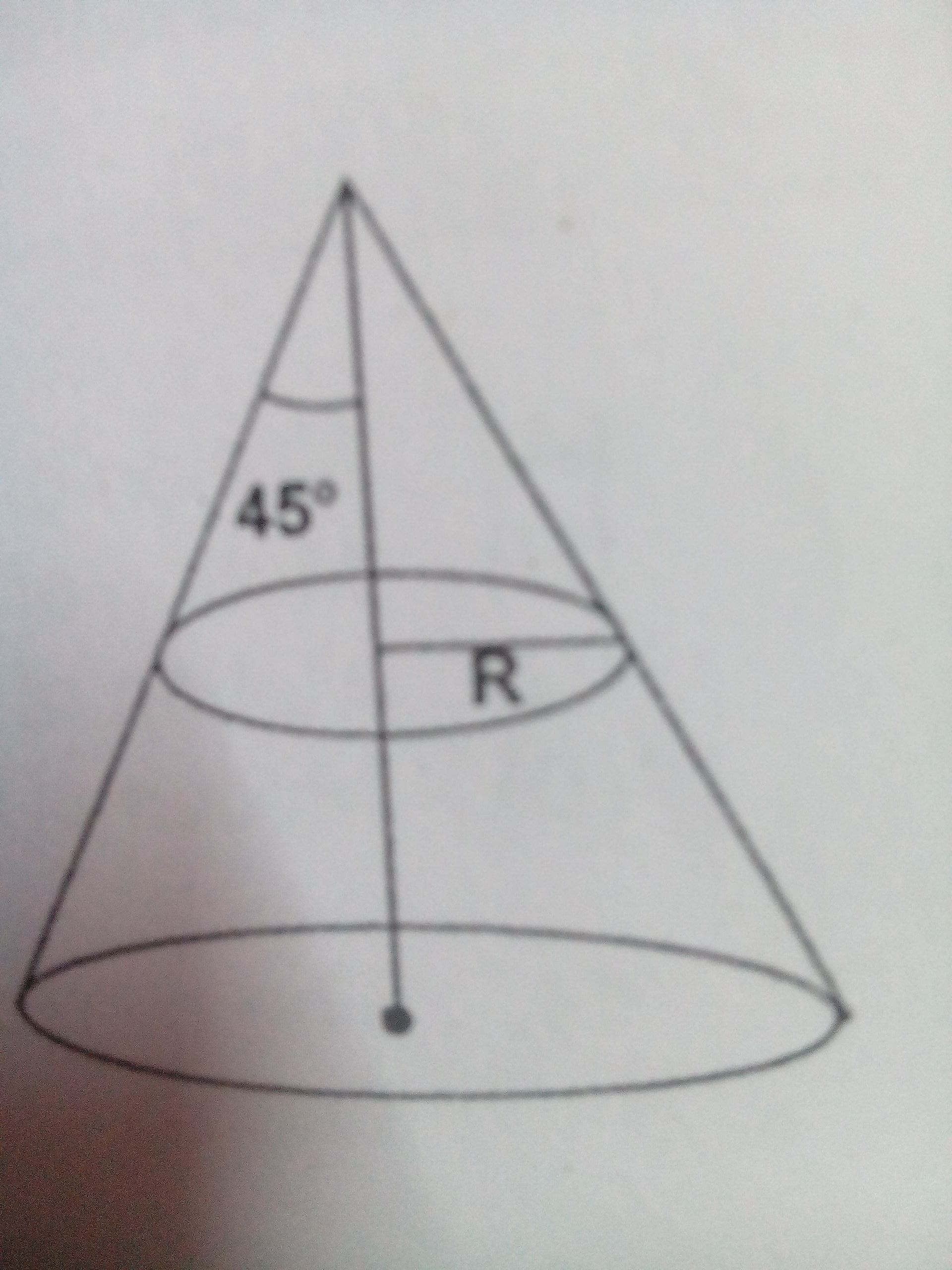
2) A ring of mass and radius rests in equilibrium on a smooth cone of semi vertical angle ,The radius of the cone is . the radius of circular cross section of the ring is .
a) What will be the tension in the ring ?
b) What will be the speed of transverse wave on the ring?
No vote yet
1 vote
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
Answer to second problem @Tanishq Varshney
Upward component of normal force balances weight of the chain. The horizontal component causes tension in ring. We can find tension in chain using the value of horizontal component.
N in the normal force acting on a small part of the ring.
dm∗g is the weight of that part and Tension acts in the ring along the tangent.
So 2N=dmg......(i)
and 2Tsin(2dθ)=2N.........(ii)
Using (i) & (ii) we get,
2Tsin(2dθ)=λRdθg where λ is the linear mass density of the ring.
So Tdθ=λRdθg
and T=2πMg
For finding the speed of the transverse wave , use vt=λT
@Kushal Patankar @Nishant Rai @Rohit Shah @Abhineet Nayyar
@satvik pandey @Raghav Vaidyanathan
Log in to reply
What are the answers?
I think the first problem's answer is 21/8s
Log in to reply
i want the method
Log in to reply
Equation of motion of first pendulum is: x1=−acos(32πt)
Equation of motion of the second pendulum is: x2=acos(72πt)
Just find t for which x1=x2 and also velocities in same direction.
answers please @Tanishq Varshney
Log in to reply
for the first one 821 and second a) 2πmg b) gr. b) part is easy once a) part is known
Log in to reply
I got second one.
Log in to reply
In the figure N in the normal force acting on a small part of the string (dm)g is the weight of that part. And Tension acts in the string along the tangent.
So N/2=dmg....(1)
and 2Tsin(2dθ)=N/2....(2)
Using (1) and (2) we get
2Tsin(2dθ)=λRdθg........................ (λ=R2πM)
So Tdθ=λRdθg
and T=R2πMR
Log in to reply
if the cone is rotated about its axis with angular velocity ω what will be the tension in the ring now??
Log in to reply
It will not change. The cone is supposed to be smooth. Hence the answer doesn't get affected by the cone spinning. Troll FIITJEE.
Log in to reply
I have a confusion. When the cone would be rotating then if we consider a reference frame moving with cone then we have to include centrifugal force on that small part while writing equations. Then how the tension would remain unaffected?
Log in to reply
Assume you have a cylindrical rod which is smooth. It is kept vertically on a smooth table. A smooth ring which just fits on the rod is put around the rod such that it lies on the table. Now, if you rotate the rod about its axis, does the ring move?
The rotation of the ring and rod are independent.
Log in to reply
Oh! I got it. The ring is not rotating with the cone! Thanks Raghav! :)
what if the cone is rough?? and we have to calculate minimum coefficient of friction so that the ring remains in equilibrium.
Log in to reply
Yes, it is possible to find the answer in this case. Actually, I did not get what you meant by: "the ring remains in equilibrium".
We can find the maximum angular velocity that the rough cone can have so that the ring doesn't slip on it for a given value of μ.
Log in to reply
the friction will act upwards along the slant height??
Log in to reply
Oh, it is more complicated than I thought. Yes, it will act upwards along slant height. Also, if the cone rotates, it will also create a torque on the ring which makes it start rotating too.
No the vertical components are balanced. I think it will act along the tangent opposite to the direction of angular velocity.
Log in to reply
may be both are possible.
is it possible to find plz reply
your answer to T is dimensionally incorrect. Correcr answer = T=2πMg
Log in to reply
I missed g in last line. It is a typo. Thanks for pointing. :)
Try this. Tension in the Ring!